近日,来自纽约市立大学的Andrea Alù教授团队提出了一种时空耦合模式理论(STCMT),能够很好地捕捉波前整形非局部超表面共振响应的关键特征。该理论框架可以定量地指导非局部超表面设计,同时保持与局部超表面框架的兼容性,为合理设计和优化各种超薄光学元件的提供了有力保障。该研究工作以“Spatio-Temporal Coupled Mode Theory for Nonlocal Metasurfaces”为题发表在《Light: Science & Applications》。
研究背景
耦合模式理论 (CMT) 是建模和理解复杂谐振电磁结构散射响应的强大工具。CMT 的核心是对系统支持的谐振模式以及将能量传入和传出谐振散射体的端口或通道进行现象学上的识别。CMT在空间域中,常用于研究波导模式及其耦合;而在时间域中,时间耦合模式理论(TCMT) 在法诺共振建模和散射矩阵构建方面取得了显著成功。该技术既可应用于局部共振,也可应用于由超表面、光子晶体板和亚波长光栅等的共振。然而,在TCMT中,模态的空间分布被忽略,模态幅度被假定为仅是时间的函数。这极大的限制了TCMT研究器件的光谱特征,使得无法捕获模式本身的详细光谱空间信息。因此,TCMT主要只用于研究无限周期光栅结构,而有限且空间变化的光栅则不能直接建模。然而,当非局域性不能被忽略时,光谱空间特性的研究极其重要。非局域超表面因其通过在动量空间中定制,以此来增强对光的控制能力而受到关注。然而,传统非局域超表面器件通常采用亚波长横向不变结构,因此其扩展谐振模式的空间特征不会逃逸出器件的近场。此时,TCMT仍然有效 [如图1(a)]。
工程非局域性可以与局部变化的特征相结合,以实现衍射非局域超表面。这些衍射非局域超表面支持高度选择性的谐振响应与定制化的空间变化相结合,能够对参与谐振的光波前进行图案化。因此,通过非周期性地调整设备上的局部扰动,谐振响应可以有效地参与任意定制的光波前。此时,TCMT无法有效分析,需要一个具有空间变化模态参数 a(x,t) 的新理论框架 [图1(b)]。如图1(c) 描绘了传统的非局域超表面,其晶胞是亚波长且横向不变的,因此与TCMT描述兼容。相反,图1(d) 描绘了一个衍射非局域超表面,其具有空间变化的方向角,与TCMT描述不兼容,需要广义的CMT模型进行分析。
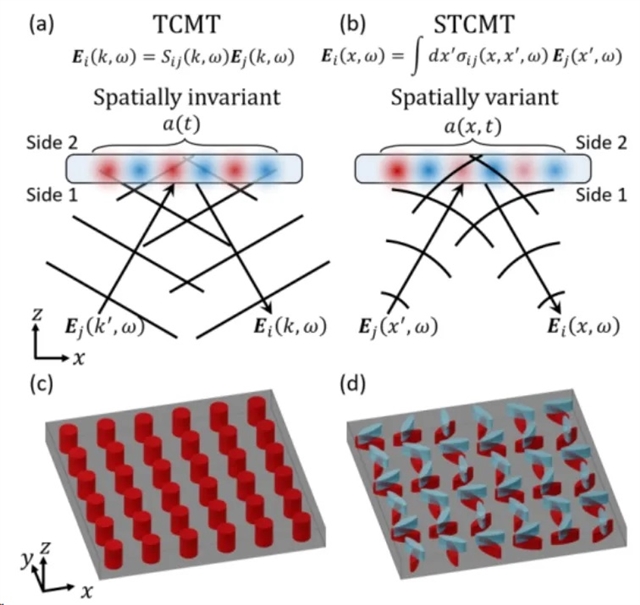
图1 耦合模式理论 (a) TCMT 对于复模态振幅 a(t) 空间不变的系统建模有效。(b) 当复模态振幅 a (x,t) 空间变化时,空间时间耦合模式理论 (STCMT) 是必要的。(c) 具有空间不变超晶胞的传统非局部超表面示例。(d) 衍射非局域超表面,具有空间变化的超晶胞。
研究创新
在这里,作者引入了一种时空耦合模式理论(STCMT),该理论扩展了时空耦合模式理论,以捕获空间变化的谐振模式。与空间选择性衍射非局部超表面的全波模拟非常一致,证明了该模型的有效性和相关性。该理论引入了非局域性长度,用于量化给定器件的非局域性程度,并确定了该参数如何直接控制空间选择性程度。文章阐明了非局域光子器件的两种不同的工作机制,由编码到器件中异常衍射的数值孔径所决定,并证明了空间选择性与支持的本征模之间的关系。虽然最近对时空耦合模式理论的研究主要集中在时变系统或传统的低对比度光栅系统上,但本工作为迅速兴起的空间变化和有限非局部超表面领域提供了广泛而迫切需要的框架。所提出的STCMT有效捕捉了空间变化谐振光子系统的基本工作机制,并为下一代光子系统的合理设计和快速计算效率分析提供了可能。
如图2所示,作者将 STCMT 应用于该示例,再现全波模拟的结果, 图2 (a) 衍射非局域超表面的原型晶胞,其中包含四个椭圆形介质柱。其中上层(蓝色)受方向角 α 调制。(b) 为 (a) 中的散射耦合模式理论近似的示意图,其中独立的散射发生在界面处,每个界面通常可以耦合到Side 1和Side 2。(c) 由 FDTD 计算的,示例超单元的动量频率响应中的反射率和反射相位。(d) 使用 TCMT 建模所得示例超单元的动量频率响应中的反射率和反射相位。(e) 使用 STCMT 对该系统进行建模,同一个超单元的空间频率域中 σ11的幅度和相位。
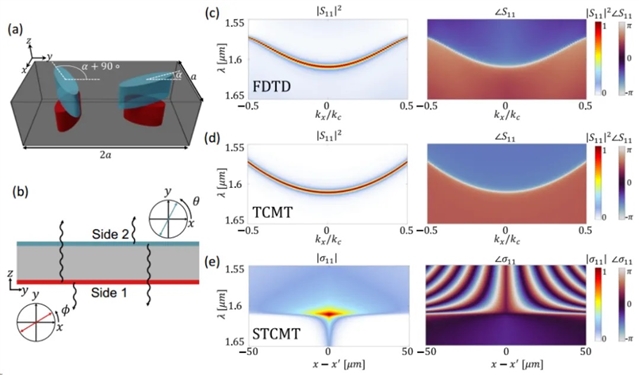
图2 全波模拟结果示例
使用离散形式的 STCMT,图 3 将没有相位梯度的情况 [图 3(a-d)] 与有相位梯度的情况[图 3(e-h)]进行了比较。图3(a) 为 kG= 0 时非局域相位梯度器件在带边频率处的谐振响应示意图。图3(b) 为S11和 S22的反射率图作为图3(a) 中器件的入射动量 k 的函数,其中虚线表示带边频率。图3(c) 为器件在带缘频率处的非局部核矩阵。图3(d) 为器件的散射矩阵。而图3(e-h)为kG= 2π/W,W=6.4 μm时运行的结果。
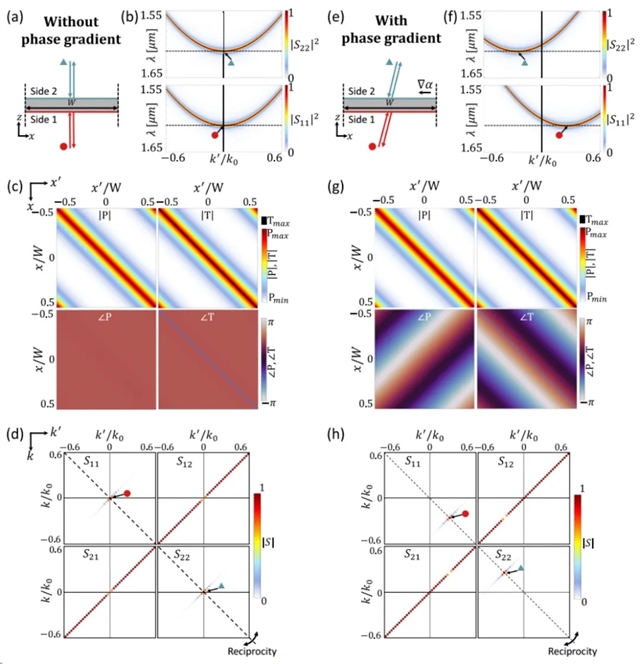
图3 针对相位梯度器件的分析
图4(a) 表示对放置在 (x0, z0) 处的点源有选择性的非局域超透镜。图4(b)和图4(c) 分别表示宽度为 W = 50μm 的超透镜的非局域反射核 P 的幅度 [图4(b)] 和相位 [图4(c)],其中q-BIC的参数为b = 0.032 μm、λ0= 1.558 μm、τr= 297 μm和 NA=0.48。图4(d)本征波和反射波,反射时显示出未改变的幅度和共轭相位分布。图4(e)为STCMT模型获得的反射率结果,图4(f)为全波模拟结果,其中为点光源在光轴(x,y,z) = (0,0,z0)位置。
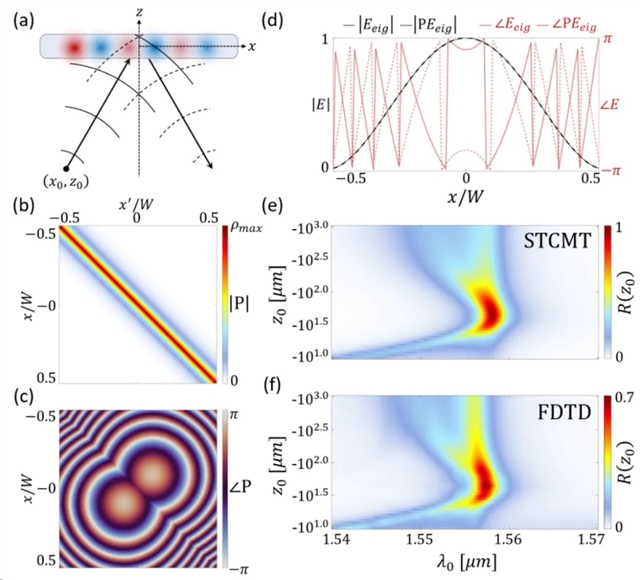
图4 非局域超构透镜
图5(a-d) 为W = 75μm但不同NA下器件的反射率,其中q-BIC 参数 b = 0.021 μm、λ0= 1.6104 μm、τr= 250 μm,点光源激发位于(x,y,z) = (0,0,z0)处。图5(e) 为对于 NA=0.1 的器件,垂直入射平面波产生的峰值反射率作为 b 和 Q 的函数。图5(f) 对于 b=0.021 的器件,垂直入射平面波产生的峰值反射率作为 NA和 Q 的函数。
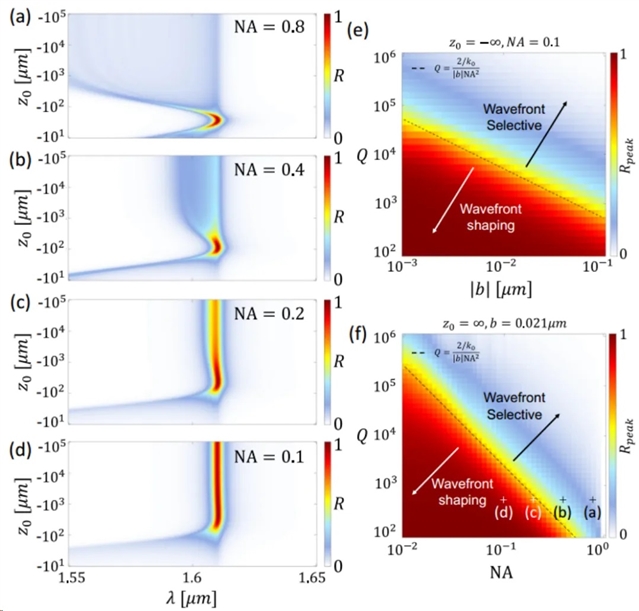
图5 非局域超构透镜的选择性
图6(a) 为热超透镜的非局域反射内核的组成部分。其中 W = 500μm 宽的热超透镜的带边频率处非局域反射核 Pnonloc 的非局域分量的(左)幅度和(中)相位,聚焦到距离f = 500μm的点(λ0= 4 μm)。(右)对应的局域反射内核Ploc。图6 (b) 对于三个例子Q因子,计算了b = 0.15 μm 的热透镜的样本点源的吸收。图6(c) 非局域性ξ0√bτr图片和峰值吸收 Apeak 关于Q因子的函数。图6(d) 放置在 z0=f 焦平面中的点源的吸收作为 Q 的函数。图6(e) 焦平面响应的半峰全宽 Δx 作为 Q 和数值孔径 NA的函数。(来源:LightScienceApplications微信公众号)
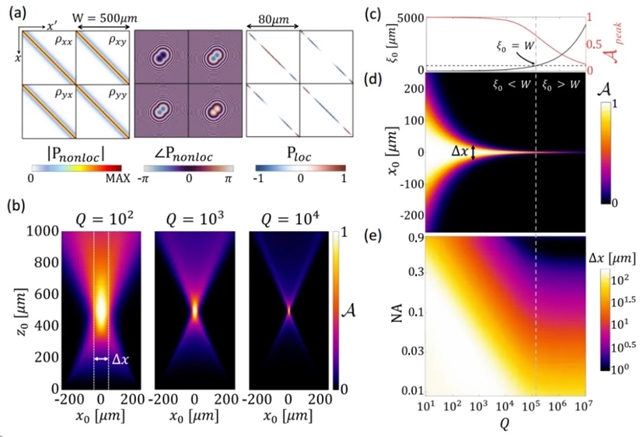
图6 热发射非局域超透镜
相关论文信息:https://doi.org/10.1038/s41377-023-01350-9
特别声明:本文转载仅仅是出于传播信息的需要,并不意味着代表本网站观点或证实其内容的真实性;如其他媒体、网站或个人从本网站转载使用,须保留本网站注明的“来源”,并自负版权等法律责任;作者如果不希望被转载或者联系转载稿费等事宜,请与我们接洽。