固体层状材料由二维或准二维层状基元沿某一个方向堆垛而成,根据基元层间相互作用类型可以分为范德华层状材料和离子型层状材料。范德华层状材料是由电中性二维基元堆垛而成,且由于层间堆垛方式、转角等不同可以展现出一系列新奇物性。最近五六年,研究人员在二维范德华层状材料数据库构建方面已经取得了重要进展,极大促进了相关领域发展。与之相比,离子型层状材料由带正和负电荷的二维基元堆垛而成,例如铁基超导体LaOFeAs由带正电[La2O2]2+和带负电[Fe2As2]2-层状基元交错排列而成。这些带电的离子型基元通常分为两类,物性决定层(如[Fe2As2]2-层)和载流子库层(如[La2O2]2+层)。选择特定的功能层和载流子库层可以实现功能导向性的材料设计和物性调控。由于离子层选择的多样性,不同的层间电子结构耦合、电荷转移等有望催生出范德华层状材料不具备的新奇物性和卓越性能。然而,目前离子层状基元缺乏高效率的全局筛选方案,阻碍了高性能、新物性离子层状材料的设计和构筑。
中国科学院物理研究所/北京凝聚态物理国家研究中心杜世萱研究团队长期致力于理论预测新型低维材料结构、表界面性质等,并提示其构效关系、规律。该团队近年来利用多尺度计算模拟方法预测了一系列具有高迁移率[J. Phys. Chem. Lett. 12, 6007 (2021)]、拓扑和超导[NPJ Comput. Mater. 8, 185 (2022)]、磁性[NPJ Comput. Mater. 6, 152 (2020), Nano Lett. 22, 3598 (2022) , NPJ Comput. Mater. 9, 50 (2023)]等物性的低维材料,构建了二维材料界面数据库[Chin. Phys. Lett., 38, 066801 (2021)]等。
最近,杜世萱研究员团队利用拓扑缩放算法(topological scaling algorithm)对现有Materials Project材料数据库中带电二维基元进行了识别,并构建了二维离子型基元数据库。他们对该数据库中的基元进行了晶系、结构原型等方面进行了分类,并初步确定了部分基元的功能性,如超导电性、磁性、拓扑等物性。随后,他们搭建了系统构建层状结构的流程,利用数据库中四方、六方、三方基元,考虑价态和晶格匹配原则,构建了3000余种不含f电子的层状结构,并对这些结构的稳定性进行了评估。通过凸包分析和声子谱计算,确定了热力学和动力学稳定、原胞尺寸较小的353个在实验上最有潜力合成的结构。
他们以几个例子展示了基于该材料数据库的在新材料、新物性发现方面的应用。在磁性材料方面,发现Na2CuIO6是双极铁磁性半导体,在自旋阀、自旋过滤等自旋电子学方面有潜在应用;同时由于体系缺乏中心反演对称性,该结构还具有谷极化特性,能够产生反常谷霍尔效应;需要强调的是,以上两种物性是其母体材料KCuIO6不具备的。在超导材料方面,发现CaAlSiF具有比其母体材料NaAlSi更高超导转变温度的超导电性。在拓扑材料方面,发现LaRhGeO在考虑自旋轨道耦合后,Γ点处Rh的dxy和dxz/dyz轨道发生了能带翻转,使体系进入拓扑非平庸态。
离子层状基元数据库的建立有助于多功能材料的构建,例如堆垛多种功能基元形成多层材料,其功能基元之间的协同效应产生的涌现现象值得进一步研究。此外,该方法可以推广到一维和零维基元,堆垛这些基元可以丰富新功能材料的设计空间。目前,该研究产生的基元数据库和新结构可以在课题组主页进行访问和查阅[http://n11.iphy.ac.cn/databases/index.html]。
以上工作以"Database Construction of Two-Dimensional Charged Building Blocks for Functional-Oriented Material Design"为题发表于Nano Lett. 23, 4634 (2023),博士后邓俊为第一作者,杜世萱研究员为通讯作者,其他作者包括潘金波副研究员和中国科学院大学博士后张艳芳。该工作得到了国家自然科学基金(61888102, 52272172, 52102193),国家重点研发计划(2021YFA1201501),科技部重点研发项目(2022YFA1204100)和中科院B类先导专项(XDB30000000)等项目的支持。(来源:中国科学院物理研究所)
相关论文信息:https://pubs.acs.org/doi/10.1021/acs.nanolett.3c01237
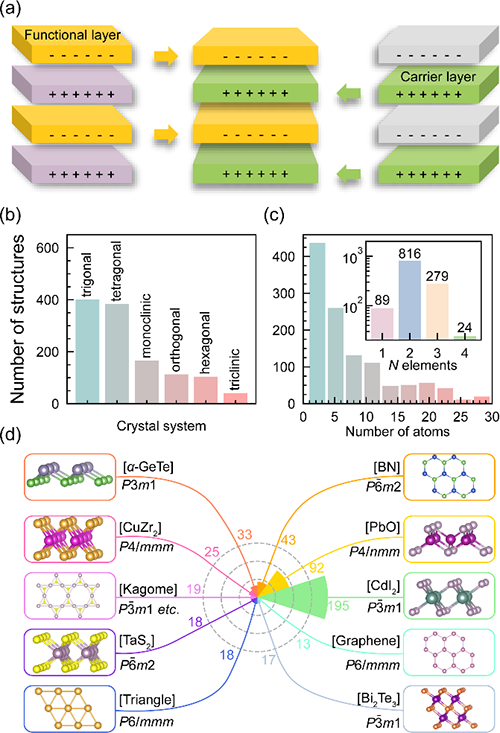
图一:由带电基元构建功能材料的示意图和带电离子型层状基元的统计
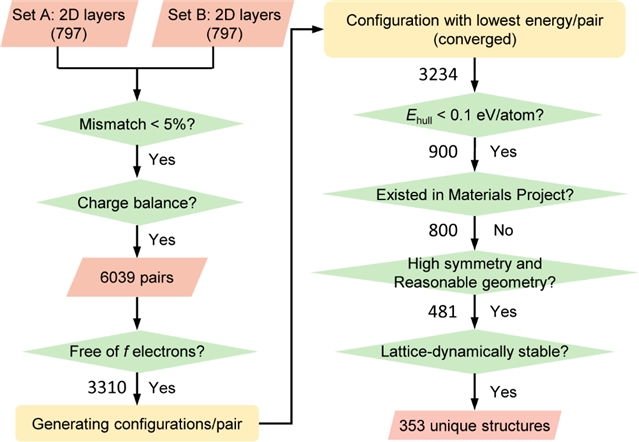
图二:离子型层状材料的设计工作流程
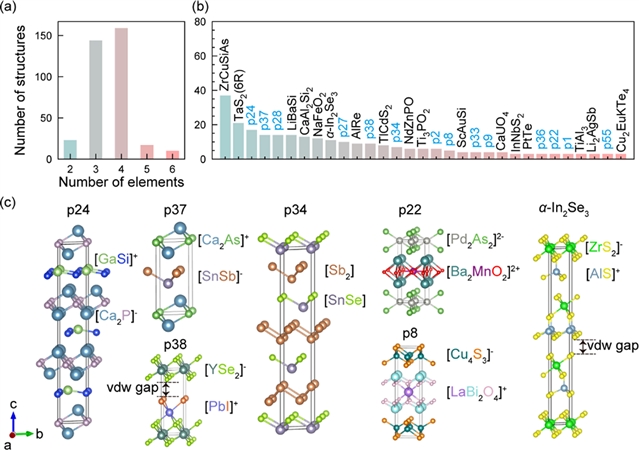
图三:新发现的353个层状材料统计和部分结构原型
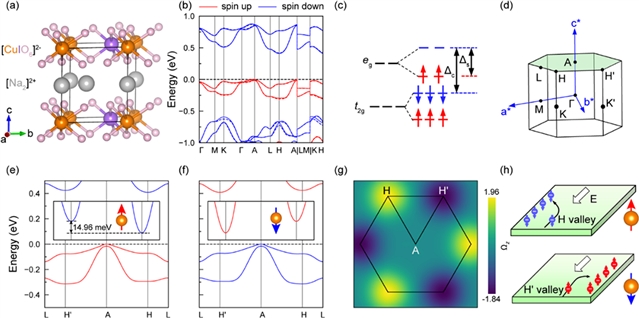
图四:Na2CuIO6的双极铁磁半导体性以及反常谷霍尔效应
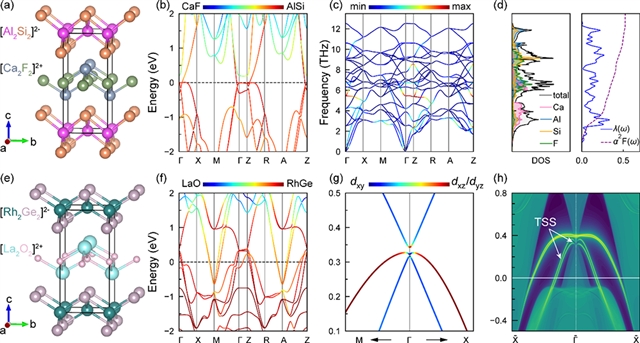
图五:CaAlSiF的超导电性和LaRhGeO的非平庸能带拓扑
特别声明:本文转载仅仅是出于传播信息的需要,并不意味着代表本网站观点或证实其内容的真实性;如其他媒体、网站或个人从本网站转载使用,须保留本网站注明的“来源”,并自负版权等法律责任;作者如果不希望被转载或者联系转载稿费等事宜,请与我们接洽。