来源：Frontiers of Engineering Management 发布时间：2024/5/13 18:34:53

选择字号：小 中 大

FEM | 城市轨道交通中断管理: 研究进展及未来方向

论文标题：Urban rail transit disruption management: Research progress and future directions

期刊：Frontiers of Engineering Management

作者：Lebing WANG, Jian Gang JIN, Lijun SUN, Der-Horng LEE

发表时间：26 Feb 2024

DOI：10.1007/s42524-023-0291-z

微信链接：点击此处阅读微信文章

作者：王乐冰^a，金建钢^a*，孙立君^b，李德纮^c*

单位：a. 上海交通大学船舶海洋与建筑工程学院；b 加拿大麦吉尔大学土木工程学院；c. 浙江大学伊利诺伊大学厄巴纳香槟校区联合学院

引用：Lebing WANG, Jian Gang JIN, Lijun SUN, Der-Horng LEE. Urban rail transit disruption management: Research progress and future directions. Frontiers of Engineering Management, 2024, 11(1): 79–91 https://doi.org/10.1007/s42524-023-0291-z

文章链接：

https://link.springer.com/article/10.1007/s42524-023-0291-z

https://journal.hep.com.cn/fem/EN/10.1007/s42524-023-0291-z

摘要：突发中断给城市轨道交通系统的运营带来相当大的挑战，主要原因包括（1）概率高，设施故障、灾害和人为破坏都会导致突发中断；（2）负面影响大，会造成大量乘客的延误；（3）频率上升，随着设施老化发生故障的可能性增加；（4）处罚力度大，城市轨道交通运营公司可能要为非正常运营支付巨额罚款。本文系统性回顾了过去十年关于城市轨道交通中断管理的相关文献，将其分为事前干预和事后应对措施两类。事前干预类的研究侧重于通过网络分析、乘客行为分析、优化防护与备用资源的部署，以及韧性网络设计来减少中断带来的负面影响。事后应对措施类研究则集中于通过优化列车运行计划调整和公共接驳服务来恢复服务。通过对这些文献整理发现，当前学者已经对事后应对方案进行了深入研究，但事前干预类的研究主要集中于分析，缺乏对能落地的解决方案的研究。因此本文提出，未来的研究可以从提高运输方式间替代性、加强城市轨道交通线路冗余性、突发中断事前预案制定以及创新性事后应对策略等方面展开。

关键词：城市轨道交通；中断管理；韧性；列车运行计划调整；公交接驳服务

1.引言

城市轨道交通具有环保、高效、高运载能力和全天候运行等优势，是许多大中型城市减轻交通拥堵的重要手段。然而，在城市轨道交通为乘客提供极大出行便利的同时，它本身也面临着各种运营挑战，包括因基础设施老化、车辆故障、轨道侵入、医疗紧急事故和极端天气等而引发的延误和服务中断（Pender等人，2012）。2017年7月，纽约地铁因轨道上存放垃圾引发了一场火灾，导致多条地铁线路出现严重延误和中断，造成9人轻伤。2022年8月，北京地铁2号线发生一起自杀事件，导致线路延误一小时。即使在准点率高达99.9%香港地铁，每年也会遭遇250余次中断。这些中断中，10%会导致延误超过30分钟（Zhang和Lo，2018；2020）。

中断对城市轨道交通系统构成严重威胁，原因如下：（1）高概率：城市轨道交通是一个复杂的系统，是大量信号、轨道、隧道和站点共同构成的庞大网络，网络中的线路之间存在复杂换乘关系。这样线路交织关系下，即使一个环节的轻微中断也可能在整个网络中产生连锁反应，从而导致城市轨道交通系统大规模延误（Tan等人，2020）;（2）严重的负面后果：城市轨道交通日常承载大量乘客，故服务中断也可能会影响大量乘客。较长时间的延误会导致乘客不满，从而对社会造成严重不利影响（Zheng等人，2022）;（3）频率增加：随着投入年份增加，基础设施老化、设施故障导致的中断频率会上升（Currie和Muir，2017）;（4）严格的处罚：在一些城市，如香港，城市轨道交通运营部门会为中断支付高额罚金，这给运营部门带来了巨大的财务负担。

因此，有效的中断管理对确保城市轨道交通系统的平稳、可靠运行至关重要，学者们也越来越将中断管理视为一个迫切解决的问题。本文对过去十年的城市轨道交通中断管理相关文献进行了深入研读与分析，总结出它们研究主题主要分成两类：事前（预防性）干预和事后（应对性）措施，如图1所示。

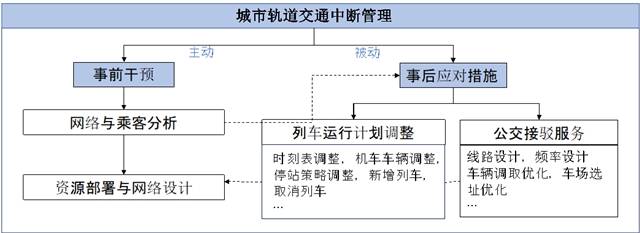
图1. 文献综述结构

事前干预包括在中断发生之前采取的行动。具体包括通过对网络特征和乘客需求的定性定量分析，洞察中断对城市轨道交通系统及乘客的影响，揭示了中断在城市轨道交通网络内的传播模式以及乘客在中断发生后行为的演变（Li等人，2020b）。基于以上分析，学者们建议运营部门可战略性地在最容易发生中断或中断后果最为显著的区域部署防护资源和备用设备。此外，少量研究认识到若能在城市轨道交通线网设计阶段就考虑未来潜在中断事件，则可建立一个高韧性的网络，从而减少由意外中断造成的延误和损失，确保城市轨道交通更顺畅的运行。

事后应对措施指的是在中断发生后采取的行动，旨在疏散乘客并迅速恢复服务。当前主流的事后应对措施包括调整受影响线路的列车运行计划和在受中断影响的区域提供临时公交接驳服务（Pender等人，2012）。学者们针对不同中断场景制定了差异化的列车运行计划调整方案，并在接驳公交路线设计、调取和车场选址等方面探索了更有效和更高效的策略。

中断对城市轨道交通系统的影响可以抽象为图2（Ghaemi等人，2017）。黑线显示了在未实施中断管理措施时城市轨道交通服务质量的变化，即一旦发生中断，服务质量会急剧下降，持续在较低水平直到中断结束（Wang等人，2021b）。事前干预是在中断发生之前主动执行的，其目标是减少中断的可能性或减轻中断对系统的影响。相反，事后应对措施在中断发生后被动执行，目的是尽可能地恢复服务。事后应对措施的制定依赖于事前阶段进行的分析，而科学合理的事后应对措施可以增强网络韧性。事前干预与事后应对措施一同构成了完善的中断管理方案，以确保城市轨道交通运营的安全、高效和可靠。

图2. 事前干预与事后措施对服务质量的提升

本文的结构如下：第2节是关于事前干预的文献综述，第3节是关于事后应对措施的文献综述，第4节回顾了事前事后结合的研究，最后在第5节对所有文献进行总结与讨论，并提出未来研究方向。

2.事前干预

对于轨道交通运营部门而言，做好事前干预，建立完备的事前预案能更主动且高效地在发生中断事件时做出反应。制定成功事前干预计划的前提是透彻把握中断对城市轨道交通系统以及乘客的影响。

2.1 网络分析

轨道交通具有网络连通性与线路关联性，多数情况下，即使一个或几个车站中断，其影响也可能扩散到整条线路，甚至整个网络。所以科学的线网特性分析十分重要，该方面的研究主要基于网络脆弱性和韧性分析展开（Chen等人，2023）。

其中，脆弱性是指被攻击或被伤害的可能性（Hong等人，2022）。网络中脆弱环节指的是最容易发生中断或中断后受影响最严重的环节（De-Los-Santos等人，2012）。Krishnakumari等人（2020）通过分析乘客轨迹，将乘客延误分解为对应的轨道段延误、初始等待时间和换乘延误，来确定单个轨道交通系统组件（如车站和轨道段）对整体乘客延误的贡献，从而识别出需要特别关注的单个组件，为运营方提供决策建议。Zhang等人（2021a）提出了基于历史事件和乘客需求的大规模数据的因果推断方法，设计了反映干扰对旅行需求、平均旅行速度和乘客流分布的因果影响的经验脆弱性指标，来评估城市轨道交通系统中各站点的脆弱性。Kopsidas和Kepaptsoglou（2022）结合中断期间的替代服务，在复杂网络理论的基础上开发了一种评估城市轨道交通站点关键性的方法，以确定哪些关键车站需要得到重点保护。以上网络分析相关文献均旨在识别出网络中脆弱环节，为后续对其进行有效防护资源部署提供决策参考。

韧性是指系统抵御外部冲击而不至于出现重大损失，以及能迅速恢复正常状态的能力（Chen等人，2023）。高韧性的城市轨道交通系统在中断发生时不会出现大幅度的服务能力下降，并能迅速恢复到正常运行状态。对于发达的城市轨道交通网络，部分线路间存在替代关系，即乘客在网络中有多种路径完成行程。这种线路之间的冗余能在中断事件发生后有力保障系统依旧具有服务能力。Xu等人（2018）提出评估网络冗余度的计算方法，解决了乘客在线网中有多少可用的有效冗余选择以及网络中有多少冗余容量这两个基本问题。Jing等人（2020）开发了一种基于路线冗余概念的方法来识别城市轨道交通系统中的关键站点，提出了平均超额临界概率，将其作为一种风险度量来计算城市轨道交通网络中每个车站的临界度。结果表明，关键车站不一定是换乘车站，而在发车间隔、客流和网络效率上重要车站也不一定是网络冗余的关键。Xu和Chopra（2022）采用复原力周期框架，分析了破坏性中断事件相关的四个生命周期阶段：准备、稳健、恢复和适应。他们提出的流量加权和空间分析可用于确定系统的复原力，研究得到结论：密集建设的车站在应对中断时具有优势，线路冗余对韧性提高有重要意义。总而言之，韧性分析倾向于从更前瞻性的角度对中断管理和网络设计提供参考建议。

2.2 乘客行为与需求分析

乘客作为交通出行的重要参与主体，也会直接受中断的影响。所以制定中断管理方案时也需参考中断给乘客带来的影响。

一方面，部分文献量化研究了中断对乘客的影响程度。Sun 等人（2016）评估了中断对乘客旅行时间的延误，研究了中断的连锁反应。Liu等人（2021）采用蒙特卡罗方法模拟了中断事件，综合客流数据和投入产出模型研究了客流损失的风险传播。客流损失包括直接客流损失，和不同线路之间换乘的间接客流损失。Eltve等人（2021）提出了一种利用智能卡数据来调查中断对乘客的长期影响新方法。

另一方面，部分文献旨在了解乘客在中断后的行为，从而掌握需求变化趋势。中断发生后，一些乘客会留在城市轨道交通系统中，而另一些乘客可能会转向其他交通方式，或者取消行程（Sun 等人，2016）。Wang等人（2014）基于复合泊松过程对受影响的乘客需求建模，区分考虑了受中断影响的乘客的直接放弃和中途背弃行为，并将其表述批量排队问题。其研究为中断发生后应对方案的制定提供研究基础。Currie and Muir（2017）调查了对墨尔本乘客对城市轨道交通中断的反应，结果显示大多数乘客愿意转乘公交接驳服务。Pnevmatikou等人（2015） 采用嵌套Logit方法来联合分析RP/SP数据，对长期服务中断期间的模式选择进行建模。Li等人（2020a）也采用嵌套式Logit模型更具体的分析了中断下乘客的出行方式转换。其嵌套结构由两层组成：上层表示方式转换选择，下层表示方式转换与否对应的旅行计划选择。研究结果表明，中断属性和个人属性是影响方式转换的重要因素。Liu等人（2021b）使用自动票务收集数据（AFC）来全面分析突发中断的影响。他们开发了一套性能指标，从列车运行、信息提供和接驳巴士的角度评估系统性能和乘客个人反应，并提出了一种推理方法量化个人对中断的反应（如旅行或不旅行，改变车站或出行方式）。研究表明中断的影响是全网性的，且中断对乘客的影响在事件结束后还会持续相当长的时间。研究同时也印证了实时信息的重要性。

2.3 资源部署

在网络性能分析与乘客行为分析的基础上，部分研究了针对如何进一步制定更加详细可行的中断干预方案。尤其在确定了线网脆弱环节之后，学者们针对防护资源的优化分配展开了研究。

An等人（2013）提出了一种可靠的应急设施选址模型，通过分析疏散资源的可用性，找到了一个最优的资源配置策略，以平衡疏散人员的风险和疏散机构的运营成本。Jin等人（2015）聚焦恶意破坏导致轨道交通中断的情景，建立了一个防御者-攻击者-用户的三层博弈论模型，可提供城市轨道交通系统抵御恶意破坏的事前保护资源分配方案。

另一种有效的通过事前资源部署应对中断的方法是增加城市交通的冗余。这确保了乘客在城市轨道交通中断发生时还有一系列可供选择的替代交通方式来完成他们的旅程（Hua和Ong，2017）。Jin等人（2014）主张从事前角度整合公交资源，以增强现有的城市轨道交通系统韧性，并开发了一个优化模型来确定最佳的地铁-公交整合运行方案。Yang等人（2017）提出了一种将乘客流量控制与临时公交接驳服务相结合的综合策略，即在高峰时段开行临时公交接驳服务缓解城市轨道交通系统的拥堵，这种情景类似于中断后城市轨道交通内部乘客的过饱和。

2.4 韧性网络设计

高韧性的城市轨道交通网络确保了系统持续高质量的运行。若能在设计阶段考虑潜在中断，提供更具有韧性的线网规划设计方案，则能从更前瞻的角度减少中断对轨道交通系统带来的冲击（Cadarso等人，2017；2018）。

当前缺乏专门针对中断情景的城市轨道交通线网设计研究，但考虑需求不确定性的网络设计仍具有参考价值（Canca等人，2019）。Moccia等人（2017）假设需求是弹性的，提出了目标是最大化运营商利润的和社会福利的公交线路设计随机优化模型。Cadarso等人（2017）提出了一个快速交通网络设计模型，从鲁棒性和风险理论的角度考虑了网络可靠性。Cadarso等人（2018）考虑乘客需求不确定性和潜在中断，提出了一种用于确定基础设施随时间的投资顺序的模型。Wang等人（2023a）研究了基于现有城市轨道交通网络的新线路设计，提出考虑需求不确定性的鲁棒优化模型。研究结果表明，在未来需求存在大幅下降的情景下，鲁棒优化模型给出的线路设计方案更加稳定和更具有竞争力，此情景与长期中断后期需求的变化类似。

此外，在设计阶段有意识地加强线路间相互替代性也可以增强韧性。在原本出行路线发生中断的情况下，乘客仍然可以通过换乘至城市轨道交通网络其他路线到达目的地。目前从这个角度出发的文献主要集中于道路网络设计（Xu等人，2021b；Zhu等人，2023），尚无考虑中断的城市轨道交通的网络设计相关研究。

3.事后应对措施

目前实际运营中，城市轨道交通突发中断发生后运营方主要任务是疏散受影响的客流，并且尽可能恢复部分服务。当前轨道交通部门采取的应对措施包括以下两种：中断线路上列车运行计划调整与在中断区间提供应急公交接驳服务。

3.1 列车运行计划调整

列车运行计划调整包括对中断后线路的时刻表重新排布、交路调整、停站策略调整、机车车辆调整、改变列车编组容量等，以尽可能恢复轨道交通服务 （Cacchiani等人，2014）。比如在2021年11月，上海轨道交通1号线莲花路至上海南站突发中断后，1号线运营交路调整为徐家汇站至富锦路站小交路，莘庄站至徐家汇站单线双向运行。

3.1.1 城市轨道交通列车运行计划调整

现实中第一时间的应对措施是轨道交通系统的内部调整，因此学者对此进行了广泛的研究。其中，部分研究考虑了乘客特征。Cadarso等人（2013）建立一个综合优化模型以解决轨道交通系统中断后列车时刻表和机车车辆调整问题，并且考虑到中断对旅客需求的影响，提出了一个基于两步法的框架，将优化模型与乘客行为模型相结合。在此基础上，Cadarso和Marín（2014）增加考虑了OD需求以刻画乘客在网络中的路径选择及方式转变，提出了最小化恢复时间、乘客不便以及调整成本的整体优化模型，对时刻表与机车车辆作出调整。Besinovic等人（2019）将列车运行计划调整、基于中断时间表的乘客路线重新规划、车站闸门控制整合在一起进行了建模。Wang等人（2018）研究了城市轨道交通乘客需求时变的情况下列车时刻表和机车车辆调整问题，他们引入了迭代非线性规划（INP）方法来解决多目标混合整数非线性规划问题。Huang 等人（2020）研究了动态乘客流量，并建立了考虑交替列车方向和短途转弯两种策略的非线性混合整数规划模型对列车运行计划调整进行优化。为了实现模型快速求解，他们提出了一种混合方法，将大M法和时间索引形式结合起来进行模型线性化，并采用两阶段方法给出实时方案。

考虑到中断事件本身的多样性，学者也针对不同规模、不同特征的中断场景提供具体的列车调整方案。Cadarso等人（2015）对于大规模中断问题，建立了一个时刻表和机车车辆的综合调整模型，其模型在制定调整计划时不仅考虑服务质量和运营成本，还着眼于恢复计划在实践中是否可以轻松实施。Xu等人（2016）考虑到双轨轨道上发生的事故，建立了一个列车运行计划调整模型以找到总延误时间最少的调整方案。Wang等人（2021b）研究了城市轨道交通线路完全堵塞情况下的时刻表和机车车辆调整问题，建立了一个复杂的多目标混合整数线性规划（MILP）模型。综合考虑时间表的偏差、（部分）取消和列车车距偏差，提出了一种两阶段方法来提高计算效率，其中在第一阶段解决较小规模的优化问题，仅考虑一组关键周转站；在第二阶段解决原始 MILP 问题，即根据第一阶段解决方案对变量进行调整。

在城市轨道交通运营中，小规模中断和细微干扰是很常见的。由于高频率的列车运行，即使是10分钟的中断也很容易传播到其他列车或线路，严重影响服务质量。Gao等人（2017）针对轨道交通运行中的细小故障提出了一个集成故障动态处理的实时自动时刻表重排策略。Chen等人（2022）探讨了动态列车调控和跳站策略，以实时应对频繁的干扰。他们开发了一个非线性规划模型，旨在最小化列车相对于正常运行的偏离和提高乘客服务质量，并进一步将其转化为混合整数二次规划模型，采用定制的模型预测控制（MPC）方法对模型高效求解。Jin 等人（2022）介绍了一种考虑峰值功率的实时列车运行计划调整方法，并通过调整行车时间和停站时间避免多列车同时加速。他们同样采用了MPC方法满足实时求解要求。

上述文献总结如表1所示。

表1. 城市轨道交通列车运行计划调整文献总结

注：ST: 短途转弯，ET: 紧急列车，CA: 取消列车，TO:双向列车使用同一轨道，CC: 列车组合调整，RT: 时刻表调整，RS: 机车车辆调整，RR: 线路调整，SP: 停站调整，OC: 运营成本，PD: 乘客延误，AD: 调整偏差，TD: 列车延误，PI: 乘客不便，OQ: 运行服务质量

3.1.2铁路列车运行计划调整

城市轨道交通包括地铁系、轻轨系、单轨、有轨电车、磁浮、自动导向轨道、市域快速轨道。许多城市在市中心区域采用地铁，而市郊部分采用轻轨与地面铁路等。鉴于城市轨道交通和传统铁路具有相似性，本节也回顾了传统铁路中断管理相关文献。

传统铁路系统具有较低的列车频率和更大的轨道灵活性，在具有平行线路和道岔的区域有更多调整空间。因此，发生中断时可以采用更丰富的策略。Louwerse和Huisman（2014）着眼于重大中断下的时刻表调整。他们探讨了整合时刻表调整、列车取消和短途转弯等策略的最佳解决方案。Zhu和Goverde（2019）将灵活停车（即跳站和加站）和灵活短途转弯三种策略创新性结合在一起，提出了一种高效且对乘客友好的列车运用计划调整模型。Zhu和Goverde（2020）提出了一个以乘客为导向的列车运用计划调整模型，该模型将列车运用计划调整和乘客重新分配整合到一个混合整数线性规划模型中，并考虑到车站容量，提供了涵盖列车时刻表调整、取消列车、灵活停车和短途转弯等策略的综合调整方案。他们为了有效地解决该模型，还提出了一种适应性固定优化（AFaO）算法。

近期研究更聚焦于特定的中断场景。Zhu和Goverde（2021）针对多中断在不同位置同时发生的场景，建立了混合整数线性规划（MILP）模型，提供了列车时刻表调整、取消、增站、灵活短途转弯等策略的优化方案。该研究采用了基于时空网络的模型，同时提出了两种在动态环境中重新安排时间表的方法:顺序方法和组合方法，以及多中断模型的滚动更新求解算法。Zhan等人（2021）研究了在列车无法通过中断的路段情况下的列车重新安排和乘客改道问题。他们也将该问题用基于时空网络的整数线性规划模型表示，使用交替乘法（ADMM）算法将模型分解为两个子问题，并进一步将两个子问题被分解成一系列的列车或乘客的最短路径问题，最后通过动态规划算法来求解。

铁路运营部门会根据中断情况进行时刻表和资源调整。与此同时，乘客也会根据个人偏好调整自己的出行路线。因此，列车调整时需要考虑乘客行为的变化。Binder等人（2017）提出了一个以乘客为导向的模型，以解决中断后的列车运行计划调整和乘客分配问题。Veelenturf等人（2017）主张可根据乘客出行选择对列车时刻表进行轻微修改，并通过对列车停站的调整来提高服务质量。van der Hurk等人（2018）在面对不确定的中断持续时间时，给乘客提供路线建议并调整机车车辆安排。其中列车运行计划会根据路线建议进行重新安排，以满足预计乘客出行需求。

上述文献总结如表2所示。

表2. 铁路列车运行计划调整文献总结

注：ST: 短途转弯，ET: 紧急列车，CA: 取消列车，RO: 列车顺序调整，RT: 时刻表调整，RS: 机车车辆调整，RR: 线路调整，SP: 停站调整，PR: 乘客路径调整，OC: 运营成本，PD: 乘客延误，AD: 调整偏差，TD: 列车延误，PI: 乘客不便，OQ: 运行服务质量

人员排班调整是传统铁路中断管理另一个关键方面。通常情况下，时刻表、机车车辆和人员排班是按顺序调整的，整体调整更高效但问题规模往往过大，不利于求解（Zhang等，2021b）。因此，一些文献着眼于单独研究人员排班调整问题。例如，Yuan等人（2022b）引入了一种基于深度优先搜索的人员排班调整方法，有效应对了实时排班调整的挑战。

3.1.3大客流疏散

客流分析得到的结论表明（Li等人，2020a），如果中断事件持续较短且轨道交通尚有部分服务能力时，选择继续乘坐轨道交通的人数较多，中断区间会累积起正常情况时更多的客流。Gao等人（2016）提出在中断恢复期，可通过跳过一些车站以加速列车的流通，从而迅速滞留的乘客。该研究考虑了过度拥挤和随时间变化的客流，提出了一个优化模型，并通过对优化模型分解和一种迭代算法求解模型。

城市轨道交通高峰时段乘客需求过度拥挤且分布不均的特点与中断情景类似，所以该领域的研究也具有一定参考价值。Niu和Zhou（2013）研究了严重拥堵情景下的轨道交通时刻表优化问题，考虑了乘客无法登上第一辆列车时需要被迫等待下一列车的情况，构建了基于动态变化的乘客需求的0-1整数优化模型。Yuan等人（2022a）的研究旨在利用有限的列车增加高峰客流需求区段的服务数量。他们以减少乘客在站台上的总等待时间为目标，建立了综合优化模型以提供双向城市轨道交通线路的列车时刻表、车辆分配和短途转弯调整方案。其中特别考虑了列车容量、掉头操作和可用列车数量，并开发了混合遗传算法来获得高质量的解决方案。

此外，从高峰期到非高峰期的过渡期内，乘客的出行需求存在巨大变化，此类情景与中断恢复期类似，相关的研究也具有方法上的参考性。Guo等人（2017）针对性研究了过渡期的列车时间表优化问题，提出了混合整数非线性规划模型以生成最佳的列车时间表，并使换乘同步事件最大化。该研究设计了一种基于粒子群优化和模拟退火（PSO-SA）的混合优化算法，以有效获得近似最优解。Zhou等人（2022）提出了一种考虑了潮汐式过饱和客流的列车时刻表与机车车辆优化调整方法，灵活运用不同的装载能力的车辆以满足不同时期（如高峰时段和非高峰时段）的不均衡客流需求。

3.2 应急公交接驳服务

对于延误时间较长（通常大于30分钟）或波及范围较大的中断情况，仅通过中断线路列车运行计划调整无法解决问题。现实中往往需要在中断区域内开行应急接驳公交来替代中断的轨道交通服务，从而疏散受影响乘客，减少出行延误（Monsuur等人，2021）。

研究表明，尽管中断后接驳公交服务从调度到运营需要一段时间，但只要安排得当，超过三分之二的乘客仍会选择搭乘接驳公交（Currie和Muir，2017）。实际运营中，接驳公交基本采用标准式接驳，即接驳公交沿着中断区间停靠每一个中断站点。同一个案例，2021年11月上海轨道交通1号线发生中断后，交通委抽调44辆公交车分别前往1号线莘庄站和徐家汇站，在莘庄站至徐家汇站采用双向对开、站站停的运行方式疏运滞站客流。接驳时间持续了1小时30分钟，疏运乘客近4000人。在现有的接驳方法基础上，为了进一步优化公交接驳效率，许多学者围绕接驳公交的调取途径、接驳公交路线与频率设计等方面展开研究，探究更加合理的公交接驳服务模式。

3.2.1 线路与频率设计

在接驳公交线路与频率设计方面，Wang等人（2016）建立了标准接驳路线的调度和设计模型，其目标是最大限度地降低公交接驳服务的总体成本。Dou等人（2019）发现采用标准式接驳时，由于终点车站泊位有限，会造成车辆的排队和拥堵问题，因此在线路规划和开行频率设计的过程中考虑了站点泊位的影响，并提出将一条平行式接驳线路分割成几段无重叠的公交短线路。

近几年，不少学者不局限于标准式接驳线路，进行了更加多元化的线路设计。Gu等人（2018）考虑到特殊站点比如客流量较大的换乘站，设计了具有跳站功能的快速接驳公交线路。Wang等人（2019）考虑了中断期间的动态客流，开发了一个多目标优化模型用于设计标准式和快速接驳公交线路，其目标是最大限度地减少乘客总等候时间、滞留乘客数量和公交车辆数量。Jin等人（2016）提出在保持公交车总数不变的情况下，在中断站到邻线非中断站但出行量特别大处引入非直观接驳线路。他们利用列生成算法生成了一组候选公交线路，并根据基于路径的多商品流模型确定了线路和开行频率的最优组合。结果表明对比仅采用标准式接驳服务，他们提出的方案能明显减少乘客的平均旅行延误。van der Hurk 等人（2016）也优化设计了标准线路和非直观线路。但与 Jin 等人（2016）不同的是，他们开发了一个基于路径的混合整数规划模型，以同时确定公交线路、频率和公交部署的最优方案。Chen和An（2021）整合了标准、短途和快速线路为乘客提供服务。他们构建了一个综合优化框架，其中，开发了一种暴力搜索方法来确定所有候选的公交路线，以及建立一个混合整数线性规划模型用于在需求时变的情况下联合优化公交线路和时间表。Wang等人（2023b）扩展了非直观路线的范围，两个受中断间接影响的非中断车站之间也可以开行非直观路线。在此研究中，接驳公交设计和乘客分配问题被表述为一个基于路径的整数线性规划模型，并基于列生成方法生成了非直观路线的集合。图3展示了上述文献中提出的各种公交接驳线路。

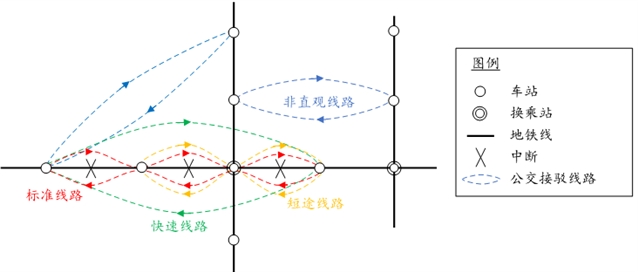
图3. 接驳公交线路

城市轨道交通的服务中断往往是临时突发的，故其本身在多个环节具有不确定性，比如中断时长，公交行驶状态，乘客需求等。Liang等人（2019）在Jin等人（2016）基础上，纳入公交旅行时间的不确定性，将模型拓展为鲁棒优化模型，得到了更加稳健的对应方案。Xu等人（2021）建立了一个分布式稳健的优化模型，用于在中断持续不确定的情况下，提供有效的公交车接驳服务、车站应对策略等，以提高系统对中断事件的容忍度。Zheng等人（2022）考虑了常规公交系统的可靠性、乘客的异质性等因素，设计了两种公交接驳方法：固定站点接驳服务和满足乘客异质性的需求响应式服务。

3.2.2 公交车辆调取

公交接驳车辆的来源问题一直是限制服务效率的关键，也是让运营部门感到棘手的难题。受到可用车数、路面交通状态、申请流程等限制，如何能快速足量地调取公交车辆，也是近年来热门研究话题。当前多数研究都是从公交车场调用闲置车辆进行公交接驳服务（Wang等人，2022）。Wang等人（2021a）提出了一个公交接驳时间表和车辆调度的双层优化模型，模型考虑了换乘客流的激增特征，并引入了乘客容忍度的概念以确定是否能满足换乘连接。其中上层解决时间表优化问题，目的是最小化乘客等待时间和换乘失败次数，下层解决车辆调度问题，目的是最小化公交车运营成本。

但城市轨道交通中断影响乘客量较大时，车场车辆可能会不足，故一些学者探索了其他调度车辆的方法。Itani等人（2020）建议在车场备用车辆不足的情况下，从邻近公交线路的终点站调度车辆。他们开发了一个公交调度优化模型，目标是最大限度地减少城市轨道交通和公交用户的总延迟时间。然而，若车场/终点站距离中断发生地较远，公交赶到花费时间过长，也不利于乘客快速疏散。Wang等人（2022）提出可将公交车来源拓展为停车场备用公交车和中断区间附近正在运行的公交车，并建立了一个整数规划模型以获得最佳调度方案。结果表明采用运行中的公交车在减少受影响乘客延误方面具有巨大潜力。

3.2.3 公交专用车场设计

部分研究着眼于设计专供突发中断情况使用的公交车场与备用车，并对其经济可行性与选址问题进行了深入探讨。Pender等人（2014）提出了一个公交部署的新概念：卫星车场或虚拟车场，即建立公交车停放区，公交车可以根据需要部署在这里，以应对突发中断等事件。该研究提出了结合旅行时间、中断事件数量以及受影响乘客规模和空间分布的卫星车场选址模型，以快速精准响应公交接驳服务需求。Pender等人（2019）继续探讨了储备纯粹用于高峰时期轨道交通中断的专用公交的经济可行性。研究结果表明，储备专用公交具有很强的净经济效益，投资应基于综合经济考量，而不是纯利益，因为储备专用公交会带来净亏损。

3.3 多方式中断管理

其他交通方式也可以辅助中断后的乘客疏散（Yin等人，2018）。Yang和Chen（2019）主张将网约车其作为疏散滞留乘客和补充公交车衔接服务的途径。他们建立了包括车辆、平台和乘客在内的服务供应链，并采用博弈论模型为中断区域内的网约车设计了补偿策略。Tan等人（2020）建议通过增加常规公交服务的频率来加强乘客疏散。Luo和Xu（2021）假定运营中的轨道交通和公交线路的剩余能力都可以为中断的乘客提供补充服务，为此构建了一个包括可用路线、现有运营公交线路和新引入的接驳公交线路的综合网络，在此基础上为乘客生成替代出行路线。

4.事前事后结合研究

除了单独的事前网络/客流分析，和事后应对措施方案制定。通过对事后应对措施效果进行评估，从而对比前后网络性能，也能为事前预案提供建议。Tessitore等人（2022）对列车运行计划调整策略进行评估，并根据当时的交通状况和中断的性质为列车调整提供了指导建议。Liu等人（2021）从公交接驳策略的角度评估了网络性能。Tang等人（2021）通过线性规划优化模型研究了城市轨道交通系统的韧性以及公交接驳服务的有效性，结果表明公交接驳可将系统恢复能力提高14%至30%。此外，Li等人（2023）提出了一种以恢复力为导向的定量评估指标，用于衡量系统在中断期间的性能，并开发了一种考虑车站拥堵的列车运行计划调整模型。研究结果为关键车站，尤其是换乘车站的容量规划提供了建议。然而，由于在进行事前事后研究时，采用的主流方法并不一致，前者强调分析，后者侧重于优化模型，结合两者的研究并不充足。

5.结论与未来研究方向

本文全面分析了过去十年有关城市轨道交通中断管理的文献，重点关注了研究方法、研究目标和研究结果。根据研究内容执行时间，本文将该领域的研究分为两类：事前干预和事后应对措施。

事前干预包括在中断发生前为减轻其不利影响而采取的措施。该领域已有丰富研究成果，包括分析城市轨道交通网络特性以确定需要加强防护的环节、探究乘客行为和中断后的需求波动、根据网络分析结果制定线路冗余和防护资源分配策略，以及高韧性网络设计。

事后措施的研究主要集中在两种常用的中断管理方法上，即列车运行计划调整和公交接驳服务。在列车运行计划调整问题上，学者们采用了多种调整策略，如调整时刻表、取消列车、短途转弯和灵活停站等，建立了各种优化模型来应对不同类型的中断，并开发了求解模型的高效算法。关于公交接驳服务，学者们提出了大量优化模型来设计高效的公交接驳路线。并探索了各种公交车资源，以实现快速响应。此外，为了进一步提高效率，部分研究建议整合各种交通方式，包括出租车、网约车、常规公交车等应对中断事件。

在最近的文献中，出现了事前事后结合的研究。主要研究思路是通过量化中断前后的网络能力来评估事后应对措施的有效性，从而为事前干预提供有价值的见解。

总而言之，在过去十年中，学者们在城市轨道交通中断管理领域开展了大量研究。这些研究中提出的方法、模型、算法和案例有助于运营部门做出明智决策，为实际中断管理提供了新思路。尽管如此，值得注意的是，目前许多城市的城市轨道交通系统运营年份并不长。例如在中国，大多数城市轨道交通都是在过去二十年内建成的，发生重大中断的情况并不频繁。因此，近期研究中提出的中断管理策略并没有全部得到实施。许多城市轨道交通系统尚未建立完善的中断预案体系，目前采用的事后应对措施也局限于简单的列车停运和标准式公交接驳服务。

所以，城市轨道交通中断管理还有很多值得深入挖掘与创新的地方。

一是当前关于事前干预的研究明显少于事后应对措施，且事前干预研究多集中于分析，能够落地的方案类成果较少。但是对于轨道交通管理部门而言，主动防范比被动应对能带来更小的负面损失。其中，防护与冗余资源有效部署能更大程度降低发生中断影响；建立完备可靠的中断预案能在增强应对效率的同时减少成本；若能从规划设计阶段就能考虑到未来中断事件，更是能增强线网韧性，持续保证系统的高质量正常运行。所以，如何从事前干预角度去解决中断问题非常关键且极具现实价值。

二是对于中断后城市轨道交通系统列车运行方案调整的研究多集中于对中断线路本身的调整，即尽量恢复中断线路的运行。但是对于高密度的轨道交通网络，仅仅只靠中断线路的调整，恢复部分服务很难达到较好的疏散效果。此外，接驳公交的调取也需要申请与调度时间，会造成大量乘客的滞留。因此，学者应探索更快速、大量的疏散措施。例如，可利用城市轨道交通线网剩余能力去疏散客流。

三是中断后大量乘客改用其他交通方式可能会对道路交通产生影响。这一领域的研究很少，未来可从中断对道路交通的影响程度以及缓解策略等方面着手展开，还可以探索轨道交通与道路交通的协作式管理方法。

最后，优化模型已被广泛应用于列车运行计划调整和公交接驳服务设计，学者们也开发了各种算法高效获得模型最优解。最近，人工智能的出现为快速求解大规模模型提供了新的机遇，故建议在未来的城市轨道交通中断管理研究中运用人工智能技术。

扫描二维码阅读原文

参考文献

An S, Cui N, Li X, Ouyang Y (2013). Location planning for transit-based evacuation under the risk of service disruptions. Transportation Research Part B: Methodological, 54: 1–16 doi:10.1016/j.trb.2013.03.002

Besinovic N, Wang Y, Zhu S, Quaglietta E, Tang T, Goverde R M P (2019). Integrated train and passenger disruption management for urban railway lines. In: IEEE Intelligent Transportation Systems Conference (ITSC). Auckland: IEEE, 3182–3187

Binder S, Maknoon Y, Bierlaire M (2017). The multi-objective railway timetable rescheduling problem. Transportation Research Part C: Emerging Technologies, 78: 78–94 doi:10.1016/j.trc.2017.02.001

Cacchiani V, Huisman D, Kidd M, Kroon L, Toth P, Veelenturf L, Wagenaar J (2014). An overview of recovery models and algorithms for real-time railway rescheduling. Transportation Research Part B: Methodological, 63: 15–37 doi:10.1016/j.trb.2014.01.009

Cadarso L, Codina E, Escudero L F, Marín A (2017). Rapid transit network design: Considering recovery robustness and risk aversion measures. Transportation Research Procedia, 22: 255–264 doi:10.1016/j.trpro.2017.03.032

Cadarso L, Escudero L F, Marín A (2018). On strategic multistage operational two-stage stochastic 0–1 optimization for the Rapid Transit Network Design problem. European Journal of Operational Research, 271(2): 577–593 doi:10.1016/j.ejor.2018.05.041

Cadarso L, Marín Á (2014). Recovery of disruptions in rapid transit networks with origin–destination demand. Procedia: Social and Behavioral Sciences, 111: 528–537 doi:10.1016/j.sbspro.2014.01.086

Cadarso L, Marín Á, Maróti G (2013). Recovery of disruptions in rapid transit networks. Transportation Research Part E: Logistics and Transportation Review, 53: 15–33 doi:10.1016/j.tre.2013.01.013

Cadarso L, Maróti G, Marín Á (2015). Smooth and controlled recovery planning of disruptions in rapid transit networks. IEEE Transactions on Intelligent Transportation Systems, 16(4): 2192–2202 doi:10.1109/TITS.2015.2399975

Canca D, De-Los-Santos A, Laporte G, Mesa J A (2019). Integrated railway rapid transit network design and line planning problem with maximum profit. Transportation Research Part E: Logistics and Transportation Review, 127: 1–30 doi:10.1016/j.tre.2019.04.007

Chen J, Jiang C, Liu X, Du B, Peng Q, Yin Y, Li B (2023). Resilience enhancement of an urban rail transit network by setting turn-back tracks: A scenario model approach. Transportation Research Record: Journal of the Transportation Research Board, in press, doi:10.1177/03611981231164066

Chen Y, An K (2021). Integrated optimization of bus bridging routes and timetables for rail disruptions. European Journal of Operational Research, 295(2): 484–498 doi:10.1016/j.ejor.2021.03.014

Chen Z, Li S, D’Ariano A, Yang L (2022). Real-time optimization for train regulation and stop-skipping adjustment strategy of urban rail transit lines. Omega, 110: 102631 doi:10.1016/j.omega.2022.102631

Currie G, Muir C (2017). Understanding passenger perceptions and behaviors during unplanned rail disruptions. Transportation Research Procedia, 25: 4392–4402 doi:10.1016/j.trpro.2017.05.322

De-Los-Santos A, Laporte G, Mesa J A, Perea F (2012). Evaluating passenger robustness in a rail transit network. Transportation Research Part C: Emerging Technologies, 20(1): 34–46 doi:10.1016/j.trc.2010.09.002

Dou X, Wang H, Meng Q (2019). Parallel shuttle bus service design for planned mass rapid transit shutdown: The Singapore experience. Transportation Research Part C: Emerging Technologies, 108: 340–356 doi:10.1016/j.trc.2019.09.022

Eltved M, Breyer N, Ingvardson J B, Nielsen O A (2021). Impacts of long-term service disruptions on passenger travel behaviour: A smart card analysis from the Greater Copenhagen area. Transportation Research Part C: Emerging Technologies, 131: 103198 doi:10.1016/j.trc.2021.103198

Gao Y, Kroon L, Schmidt M, Yang L (2016). Rescheduling a metro line in an over-crowded situation after disruptions. Transportation Research Part B: Methodological, 93: 425–449 doi:10.1016/j.trb.2016.08.011

Gao Y, Yang L, Gao Z (2017). Real-time automatic rescheduling strategy for an urban rail line by integrating the information of fault handling. Transportation Research Part C: Emerging Technologies, 81: 246–267 doi:10.1016/j.trc.2017.06.005

Ghaemi N, Cats O, Goverde R M P (2017). Railway disruption management challenges and possible solution directions. Public Transport, 9(1–2): 343–364 doi:10.1007/s12469-017-0157-z

Gu W, Yu J, Ji Y, Zheng Y, Zhang H M (2018). Plan-based flexible bus bridging operation strategy. Transportation Research Part C: Emerging Technologies, 91: 209–229 doi:10.1016/j.trc.2018.03.015

Guo X, Sun H J, Wu J J, Jin J G, Zhou J, Gao Z Y (2017). Multiperiod-based timetable optimization for metro transit networks. Transportation Research Part B: Methodological, 96: 46–67 doi:10.1016/j.trb.2016.11.005

Hong W T, Clifton G, Nelson J D (2022). Rail transport system vulnerability analysis and policy implementation: Past progress and future directions. Transport Policy, 128: 299–308 doi:10.1016/j.tranpol.2022.02.004

Hua W, Ong G P (2017). Network survivability and recoverability in urban rail transit systems under disruption. IET Intelligent Transport Systems, 11(10): 641–648 doi:10.1049/iet-its.2017.0102

Huang Y, Mannino C, Yang L, Tang T (2020). Coupling time-indexed and big-M formulations for real-time train scheduling during metro service disruptions. Transportation Research Part B: Methodological, 133: 38–61 doi:10.1016/j.trb.2019.12.005

Itani A, Srikukenthiran S, Shalaby A (2020). Capacity-constrained bus bridging optimization framework. Transportation Research Record: Journal of the Transportation Research Board, 2674(5): 600–612 doi:10.1177/0361198120917399

Jin B, Feng X, Wang Q, Sun P (2022). Real-time train regulation method for metro lines with substation peak power reduction. Computers & Industrial Engineering, 168: 108113 doi:10.1016/j.cie.2022.108113

Jin J G, Lu L, Sun L, Yin J (2015). Optimal allocation of protective resources in urban rail transit networks against intentional attacks. Transportation Research Part E: Logistics and Transportation Review, 84: 73–87 doi:10.1016/j.tre.2015.10.008

Jin J G, Tang L C, Sun L, Lee D H (2014). Enhancing metro network resilience via localized integration with bus services. Transportation Research Part E: Logistics and Transportation Review, 63: 17–30 doi:10.1016/j.tre.2014.01.002

Jin J G, Teo K M, Odoni A R (2016). Optimizing bus bridging services in response to disruptions of urban transit rail networks. Transportation Science, 50(3): 790–804 doi:10.1287/trsc.2014.0577

Jing W, Xu X, Pu Y (2020). Route redundancy-based approach to identify the critical stations in metro networks: A mean-excess probability measure. Reliability Engineering & System Safety, 204: 107204 doi:10.1016/j.ress.2020.107204

Kopsidas A, Kepaptsoglou K (2022). Identification of critical stations in a metro system: A substitute complex network analysis. Physica A, 596: 127123 doi:10.1016/j.physa.2022.127123

Krishnakumari P, Cats O, van Lint H (2020). Estimation of metro network passenger delay from individual trajectories. Transportation Research Part C: Emerging Technologies, 117: 102704 doi:10.1016/j.trc.2020.102704

Kroon L, Maróti G, Nielsen L (2015). Rescheduling of railway rolling stock with dynamic passenger flows. Transportation Science, 49(2): 165–184 doi:10.1287/trsc.2013.0502

Li B, Yao E, Yamamoto T, Huan N, Liu S (2020a). Passenger travel behavior analysis under unplanned metro service disruption: Using stated preference data in Guangzhou, China. Journal of Transportation Engineering, Part A: Systems, 146(2): 04019069 doi:10.1061/JTEPBS.0000308

Li B, Yao E, Yamamoto T, Tang Y, Liu S (2020b). Exploring behavioral heterogeneities of metro passenger’s travel plan choice under unplanned service disruption with uncertainty. Transportation Research Part A: Policy and Practice, 141: 294–306 doi:10.1016/j.tra.2020.09.009

Li Z, Yin J, Chai S, Tang T, Yang L (2023). Optimization of system resilience in urban rail systems: Train rescheduling considering congestions of stations. Computers & Industrial Engineering, 185: 109657 doi:10.1016/j.cie.2023.109657

Liang J, Wu J, Qu Y, Yin H, Qu X, Gao Z (2019). Robust bus bridging service design under rail transit system disruptions. Transportation Research Part E: Logistics and Transportation Review, 132: 97–116 doi:10.1016/j.tre.2019.10.008

Liu K, Zhu J, Wang M (2021a). An event-based probabilistic model of disruption risk to urban metro networks. Transportation Research Part A: Policy and Practice, 147: 93–105 doi:10.1016/j.tra.2021.03.010

Liu T, Ma Z, Koutsopoulos H N (2021b). Unplanned disruption analysis in urban railway systems using smart card data. Urban Rail Transit, 7(3): 177–190 doi:10.1007/s40864-021-00150-x

Louwerse I, Huisman D (2014). Adjusting a railway timetable in case of partial or complete blockades. European Journal of Operational Research, 235(3): 583–593 doi:10.1016/j.ejor.2013.12.020

Luo C, Xu L (2021). Railway disruption management: Designing bus bridging services under uncertainty. Computers & Operations Research, 131: 105284 doi:10.1016/j.cor.2021.105284

Moccia L, Giallombardo G, Laporte G (2017). Models for technology choice in a transit corridor with elastic demand. Transportation Research Part B: Methodological, 104: 733–756 doi:10.1016/j.trb.2017.06.001

Monsuur F, Enoch M, Quddus M, Meek S (2021). Modelling the impact of rail delays on passenger satisfaction. Transportation Research Part A: Policy and Practice, 152: 19–35 doi:10.1016/j.tra.2021.08.002

Niu H, Zhou X (2013). Optimizing urban rail timetable under time-dependent demand and oversaturated conditions. Transportation Research Part C: Emerging Technologies, 36: 212–230 doi:10.1016/j.trc.2013.08.016

Pender B M, Currie G, Delbosc A R, Shiwakoti N (2012). Planning for the unplanned: An international review of current approaches to service disruption management of railways. In: Australasian Transport Research Forum. Perth, 1–17

Pender B, Currie G, Delbosc A, Shiwakoti N (2014). Improving bus bridging responses via satellite bus reserve locations. Journal of Transport Geography, 34: 202–210 doi:10.1016/j.jtrangeo.2013.12.007

Pender B, Currie G, Shiwakoti N, Delbosc A (2015). Economic viability of bus bridging reserves for fast response to unplanned passenger rail disruption. Transportation Research Record: Journal of the Transportation Research Board, 2537(1): 13–22 doi:10.3141/2537-02

Pnevmatikou A M, Karlaftis M G, Kepaptsoglou K (2015). Metro service disruptions: How do people choose to travel? Transportation, 42(6): 933–949 doi:10.1007/s11116-015-9656-4

Sun H, Wu J, Wu L, Yan X, Gao Z (2016). Estimating the influence of common disruptions on urban rail transit networks. Transportation Research Part A: Policy and Practice, 94: 62–75 doi:10.1016/j.tra.2016.09.006

Tan Z, Xu M, Meng Q, Li Z C (2020). Evacuating metro passengers via the urban bus system under uncertain disruption recovery time and heterogeneous risk-taking behaviour. Transportation Research Part C: Emerging Technologies, 119: 102761 doi:10.1016/j.trc.2020.102761

Tang J, Xu L, Luo C, Ng T S A (2021). Multi-disruption resilience assessment of rail transit systems with optimized commuter flows. Reliability Engineering & System Safety, 214: 107715 doi:10.1016/j.ress.2021.107715

Tessitore M L, Samà M, D’Ariano A, Hélouet L, Pacciarelli D (2022). A simulation-optimization framework for traffic disturbance recovery in metro systems. Transportation Research Part C: Emerging Technologies, 136: 103525 doi:10.1016/j.trc.2021.103525

van der Hurk E, Koutsopoulos H N, Wilson N, Kroon L G, Maróti G (2016). Shuttle planning for link closures in urban public transport networks. Transportation Science, 50(3): 947–965 doi:10.1287/trsc.2015.0647

van der Hurk E, Kroon L, Maróti G (2018). Passenger advice and rolling stock rescheduling under uncertainty for disruption management. Transportation Science, 52(6): 1391–1411 doi:10.1287/trsc.2017.0759

Veelenturf L P, Kroon L G, Maróti G (2017). Passenger oriented railway disruption management by adapting timetables and rolling stock schedules. Transportation Research Part C: Emerging Technologies, 80: 133–147 doi:10.1016/j.trc.2017.04.012

Wang J, Yuan Z, Cao Z, Lu Z (2021a). Optimal bus bridging schedule with transfer passenger demand during disruptions of urban rail transit. Journal of Transportation Engineering, Part A: Systems, 147(10): 04021071 doi:10.1061/JTEPBS.0000568

Wang J, Yuan Z, Yin Y (2019). Optimization of bus bridging service under unexpected metro disruptions with dynamic passenger flows. Journal of Advanced Transportation, 6965728 doi:10.1155/2019/6965728

Wang L, Jin J G, Sibul G, Wei Y (2023a). Designing metro network expansion: Deterministic and robust optimization models. Networks and Spatial Economics, 23(1): 317–347 doi:10.1007/s11067-022-09584-7

Wang X, Jin J G, Sun L (2022). Real-time dispatching of operating buses during unplanned disruptions to urban rail transit system. Transportation Research Part C: Emerging Technologies, 139: 103696 doi:10.1016/j.trc.2022.103696

Wang Y, D’Ariano A, Yin J, Meng L, Tang T, Ning B (2018). Passenger demand oriented train scheduling and rolling stock circulation planning for an urban rail transit line. Transportation Research Part B: Methodological, 118: 193–227 doi:10.1016/j.trb.2018.10.006

Wang Y, Guo J, Currie G, Ceder A, Dong W, Pender B (2014). Bus bridging disruption in rail services with frustrated and impatient passengers. IEEE Transactions on Intelligent Transportation Systems, 15(5): 2014–2023 doi:10.1109/TITS.2014.2307859

Wang Y, Yan X, Zhou Y, Zhang W (2016). A feeder-bus dispatch planning model for emergency evacuation in urban rail transit corridors. PLoS One, 11(9): e0161644 doi:10.1371/journal.pone.0161644

Wang Y, Zhao K, D’Ariano A, Niu R, Li S, Luan X (2021b). Real-time integrated train rescheduling and rolling stock circulation planning for a metro line under disruptions. Transportation Research Part B: Methodological, 152: 87–117 doi:10.1016/j.trb.2021.08.003

Wang Y, Zhou Y, Yang H, Yan X (2023b). Integrated optimization of bus bridging service design and passenger assignment in response to urban rail transit disruptions. Transportation Research Part C: Emerging Technologies, 150: 104098 doi:10.1016/j.trc.2023.104098

Xu L, Ng T S, Costa A (2021a). Optimizing disruption tolerance for rail transit networks under uncertainty. Transportation Science, 55(5): 1206–1225 doi:10.1287/trsc.2021.1040

Xu X, Chen A, Jansuwan S, Yang C, Ryu S (2018). Transportation network redundancy: Complementary measures and computational methods. Transportation Research Part B: Methodological, 114: 68–85 doi:10.1016/j.trb.2018.05.014

Xu X, Chen A, Xu G, Yang C, Lam W H K (2021b). Enhancing network resilience by adding redundancy to road networks. Transportation Research Part E: Logistics and Transportation Review, 154: 102448 doi:10.1016/j.tre.2021.102448

Xu X, Li K, Yang L (2016). Rescheduling subway trains by a discrete event model considering service balance performance. Applied Mathematical Modelling, 40(2): 1446–1466 doi:10.1016/j.apm.2015.06.031

Xu Z, Chopra S S (2022). Network-based assessment of metro infrastructure with a spatial–temporal resilience cycle framework. Reliability Engineering & System Safety, 223: 108434 doi:10.1016/j.ress.2022.108434

Yang J, Jin J G, Wu J, Jiang X (2017). Optimizing passenger flow control and bus-bridging service for commuting metro lines. Computer-Aided Civil and Infrastructure Engineering, 32(6): 458–473 doi:10.1111/mice.12265

Yang Z, Chen X (2019). Compensation decisions on disruption recovery service in urban rail transit. Promet, 31(4): 367–375 doi:10.7307/ptt.v31i4.2985

Yin H, Wu J, Sun H, Qu Y, Yang X, Wang B (2018). Optimal bus-bridging service under a metro station disruption. Journal of Advanced Transportation, 2758652 doi:10.1155/2018/2758652

Yuan J, Gao Y, Li S, Liu P, Yang L (2022a). Integrated optimization of train timetable, rolling stock assignment and short-turning strategy for a metro line. European Journal of Operational Research, 301(3): 855–874 doi:10.1016/j.ejor.2021.11.019

Yuan J, Jones D, Nicholson G (2022b). Flexible real-time railway crew rescheduling using Depth-first search. Journal of Rail Transport Planning & Management, 24: 100353 doi:10.1016/j.jrtpm.2022.100353

Zhan S, Wong S C, Shang P, Peng Q, Xie J, Lo S M (2021). Integrated railway timetable rescheduling and dynamic passenger routing during a complete blockage. Transportation Research Part B: Methodological, 143: 86–123 doi:10.1016/j.trb.2020.11.006

Zhang N, Graham D J, Hörcher D, Bansal P (2021a). A causal inference approach to measure the vulnerability of urban metro systems. Transportation, 48(6): 3269–3300 doi:10.1007/s11116-020-10152-6

Zhang S, Lo H K (2018). Metro disruption management: Optimal initiation time of substitute bus services under uncertain system recovery time. Transportation Research Part C: Emerging Technologies, 97: 409–427 doi:10.1016/j.trc.2018.11.001

Zhang S, Lo H K (2020). Metro disruption management: Contracting substitute bus service under uncertain system recovery time. Transportation Research Part C: Emerging Technologies, 110: 98–122 doi:10.1016/j.trc.2019.11.010

Zhang S, Lo H K, Ng K F, Chen G (2021b). Metro system disruption management and substitute bus service: A systematic review and future directions. Transport Reviews, 41(2): 230–251 doi:10.1080/01441647.2020.1834468

Zheng S, Liu Y, Lin Y, Wang Q, Yang H, Chen B (2022). Bridging strategy for the disruption of metro considering the reliability of transportation system: Metro and conventional bus network. Reliability Engineering & System Safety, 225: 108585 doi:10.1016/j.ress.2022.108585

Zhou H, Qi J, Yang L, Shi J, Mo P (2022). Joint optimization of train scheduling and rolling stock circulation planning with passenger flow control on tidal overcrowded metro lines. Transportation Research Part C: Emerging Technologies, 140: 103708 doi:10.1016/j.trc.2022.103708

Zhu J, Xu X, Wang Z (2023). Economic evaluation of redundancy design for transportation networks under disruptions: Framework and case study. Transport Policy, 142: 70–83 doi:10.1016/j.tranpol.2023.08.004

Zhu Y, Goverde R M P (2019). Railway timetable rescheduling with flexible stopping and flexible short-turning during disruptions. Transportation Research Part B: Methodological, 123: 149–181 doi:10.1016/j.trb.2019.02.015

Zhu Y, Goverde R M P (2020). Integrated timetable rescheduling and passenger reassignment during railway disruptions. Transportation Research Part B: Methodological, 140: 282–314 doi:10.1016/j.trb.2020.09.001

Zhu Y, Goverde R M P (2021). Dynamic railway timetable rescheduling for multiple connected disruptions. Transportation Research Part C: Emerging Technologies, 125: 103080 doi:10.1016/j.trc.2021.103080

推荐阅读

1.FEM Mar 2024, Volume 11 Issue1内容摘要

2.FEM Dec 2023, Volume 10 Issue 4 内容摘要

3.FEM Sep 2023, Volume 10 Issue 3 内容摘要

4.FEM Jun 2023, Volume 10 Issue 2内容摘要

5.FEM 2023, Volume 10 Issue 1 后疫情时代供应链韧性的提升专题内容摘要

6.大坡度螺旋隧道硬岩掘进机“北山1号”装备技术创新

7.高铁企业国际声誉的形成机理

8.“海斗一号”全海深自主遥控水下机器人研制与万米深潜

9.白鹤滩水电站工程建设关键技术创新

10.复兴号动车组

11.易逝医疗资源管理文献综述

12.共享单车系统的需求可预测性：一项站点级别的分析

13.中国公路交通的直接能源回弹效应

《前沿》系列英文学术期刊

由教育部主管、高等教育出版社主办的《前沿》（Frontiers）系列英文学术期刊，于2006年正式创刊，以网络版和印刷版向全球发行。系列期刊包括基础科学、 、工程技术和人文社会科学四个主题，是我国覆盖学科最广泛的英文学术期刊群，其中13种被SCI收录，其他也被A&HCI、Ei、MEDLINE或相应学科国际权威检索系统收录，具有一定的国际学术影响力。系列期刊采用在线优先出版方式，保证文章以最快速度发表。

中国学术前沿期刊网

http://journal.hep.com.cn