来源：Frontiers of Engineering Management 发布时间：2024/2/5 13:52:09

选择字号： 小 中 大

FEM | 共享单车系统的需求可预测性：一项站点级别的分析

论文标题：Understanding the demand predictability of bike share systems: A station-level analysis（共享单车系统的需求可预测性：一项站点级别的分析）

期刊：Frontiers of Engineering Management

作者：Zhuoli YIN, Kendrick HARDAWAY, Yu FENG, Zhaoyu KOU, Hua CAI

发表时间：15 Dec 2023

DOI：10.1007/s42524-023-0279-8

微信链接：点击此处阅读微信文章

作者：尹卓立¹，Kendrick Hardaway², Feng Yu³, 寇兆宇¹，才华^1,2,*

单位：1. 美国普渡大学工业工程学院；2. 美国普渡大学环境与生态工程学院；3. 美国密西根大学环境与可持续发展学院

* 通讯作者，邮箱：huacai@purdue.edu

引用：

Zhuoli YIN, Kendrick HARDAWAY, Yu FENG, Zhaoyu KOU, Hua CAI. Understanding the demand predictability of bike share systems: A station-level analysis. Front. Eng, 2023, 10(4): 551–565https://doi.org/10.1007/s42524-023-0279-8

文章链接：

https://journal.hep.com.cn/fem/EN/10.1007/s42524-023-0279-8

https://link.springer.com/article/10.1007/s42524-023-0279-8

导语：预测共享单车系统（BSSs）的使用需求对于现有BSS的管理和新BSS的规划都至关重要。目前研究人员主要关注在提高预测准确性和分析影响需求的因素上，却很少有研究考察所观测到的各站点共享单车需求的内在随机性以及各个单一站点的共享单车需求在多大程度上是可预测的。针对这一研究需求，我们使用了位于美国芝加哥的Divvy共享单车一年的数据，测量了需求的熵, 并量化了站点级别共享单车需求的可预测性。此外，为了验证这些可预测性度量可以表征预测模型的性能，我们采用了两种常用的需求预测模型对各站点的共享单车需求进行预测，并将其预测准确度与计算的熵和可预测性进行比较。此外，我们还探究了城市和系统特定的时不变特征会如何影响熵和可预测性，以便在没有可用的历史需求数据的情况下为估算这两项度量提供信息。我们的结果表明，不同站点的需求的熵和可预测性呈两极分化，一些站点表现出高不确定性（低可预测性为0.65），而其他站点几乎没有借出需求的不确定性（高可预测性约为1.0）。我们还验证了，在给定一系列共享单车使用需求的情况下，熵和可预测性是预测误差的先验无模型指标。最后，我们确定了影响站点级别熵和可预测性的关键因素包括人均收入、空间偏心率和站点附近的停车场数量。本文的研究结果为BSS共享单车需求预测提供了量化的基础，这有助于决策者和系统运营商预见他们所用预测模型中对于现有站点和新站点在站点层面的不同误差。

关键词：共享单车系统，需求预测，预测误差，机器学习，熵

1.介绍

共享单车系统(BSS)市场近年来迅速扩大， 预计到 2030年将增长三倍(Fishman 和 Allan, 2019 ;Straits Research, 2021)。传统的 BSS是基于站点的，允许用户在指定地点取走和归还自行车(Kou 和 Cai, 2019) 。BSS允许用户根据需要付费或免费使用自行车，这提供了方便和易得的出行选择，特别是对于他们的第一/最后一公里旅行(Bachand -Marleau 等人，2012;Fishman ，2016) 。作为共享经济的一部分和作为私人汽车短途旅行的可行替代，BSS还具有减少温室气体排放的潜力 (Shaheen et al.，2010;Kou 等，2020;Zhou et al.，2023)。然而，如果 BSS没有得到很好的规划或管理， 这些益处可能仍然无法实现。未经规划或管理的 BSS可能导致供应过剩或不足、停车不便、服务水平较低、街道安全问题以及不够理想的业务运营(Regue 和 Recker, 2014;Chen et al. ，2016)。BSS的快速增长和基于智能的前瞻性设计的必要性促使研究人员研究这些系统的实现和改进(Luo et al.，2020; Kou和Cai，2021a)。

站点的需求预测是BSS规划和管理基础 。由于BSS需求的时空不平衡，BSS在不同站点之间经常出现自行车供应不足或供过于求的差异(Li et al.,2015; Chen 等人, 2016)。不准确的需求预测会导致自行车再平衡不当、运营成本增加 、用户满意度降低以及更多的温室气体排放。因此，系统运营商和研究人员对预测 BSS 站的需求给予了极大的关注(El-Assi et al., 2017; Hyland et al., 2018; Zhou等人,2018; Kou和Cai, 20121b)。

现有的需求预测研究使用传统的回归、机器学习或深度学习模型以不同的方式预 测 BSS 需求。例如，mchardon和Caruso(2015)使用基于线性回归的方法，使用六个城市的站点级数据估计每日BSS行程的需求。Hulot 等人(2018)使用线性回归和机器学习模型来预测每小时的需求，并推荐如何定期重新平衡自行车的间隔时间。基于卷积神经网络 的模型已被用于预测车站和站点级每小时需求的自行车流入和流出(Chai et al.，2018;Lin 等人，2018;Yu et al.，2018)。基于聚类的回归已被用于预测具有相似特征的站点的自行车使用和归还，并预测全程范围内的自行车使用情况(Chen 等人，2016; Jia et al.， 2019; Li 和郑，2020)。此外，一些研究研究了残差校正，以揭示时间序列数据中的隐藏随机性，以提高预测(Kim et al.，2022;Zheng 等人, 2023)。在现有模型中，为了提高预测精度，之前的研究还整合了时空变量来分析它们在影响需求中的作用。Bao 等人(2017) 通过结合智能卡数据和兴趣点(POIs) 研究了共享单车的出行模式和出行目的。Zhou(2015)和 Lin等(2020)揭示了共享单车行为的时空模式，并确定了建筑环境等因素对共享单车出行需求的影响。

除了时空信息外，各种特征也被纳入了需求预测。Yang et al. (2016;2019)使用动态网络、时间因素和天气创建了一个概率时空模型。Hulot 等人(2018)使用线性回归和机器学习模型来使用时间和天气变量预测了需求。Singhvi等人(2015)在其配对模型中使用了时 间、人口和天气因素。Chen 等人(2016)在基于聚类的预测中使用了时间和天气因素，并且增加了社会事件 (如城市节日、游行或交通事故)。尽管需求预测技术取得了进步，但现有的研究主要集中在如何提升需求预测上。需求预测的准确性只有在预测模型被开发出来之后才知道，并且需要广泛的来自研究人员的特定领域特征工程。现有的研究都没有涉及车站需求的基本可预测性，并且在理解内在随机性(即由于天气条件和人类行为等不可预测因素而导致的BSS需求的内在变化)如何决定未来需求预测的极限方面存在空白。通过了 解需求水平的支配随机性，系统操作员和城市管理者可以更好地管理和维护站点。与此同时，很少有研究评估时不变决定因素如何塑造单个车站需求模式的随机性。这些时不变的决定因素本质上表征了城市不同区域的功能，也塑造了共享单车站点之间的异质性。与依赖时间的因素(包括季节性和独特事件)相比，时不变因素随着时间的推移相对稳定。在研究解释这种随机性的变量方面存在研究空白，而通过这种随机性，我们可以获得关于异质站点级别的需求可预测性的知识，甚至在城市启动BSS之前。

为了评估预测模型的准确性，目前的需求预测研究主要是应用单一模型于整个系统，并在系统层面上评估预测模型的性能。这些研究依赖于站点级别的数据，并使用诸如均方根误差（RMSE）和平均绝对百分比误差（MAPE）之类的评估指标，但仅研究系统级别的聚合后的结果可能无法捕捉车站间的变化和异常情况，从而弱化了对站点级别预测性能的局部理解（Li等，2015年；Médard de Chardon和Caruso，2015年；Singhvi等，2015年；El Sibai等，2018年；Liu等，2022年）。例如，站点级别的理解对于站点级别的再平衡和维护高效系统运行至关重要。因此，在关注全局平均性能之外，存在一个知识空白，即预测错误在细颗粒度下如何偏离，以及需求的固有可预测性在各个站点之间是如何变化的（He和Shin，2020年）。

为了解决上述研究空白，本研究基于信息论中的熵和可预测性，量化了时间序列共享单车借出需求在各个站点的随机性和可预测性。这两个指标的计算是基于一年的数据，可以捕捉相对长期的以及季节性变化。为了测试我们度量的有效性，我们将站点级别的熵和可预测性与两个基准预测模型——自回归移动平均（ARMA）和XGBoost的实证预测性能进行了比较。这建立了一个从基于模型的准确性/误差到无模型测量的可行映射，允许在不需要先验的特征工程和预测算法的情况下预期需求的预测性能。此外，为了进一步研究城市的时不变因素如何影响BSS需求的内在随机性，本工作使用随机森林回归模型（Random forest regression model）来识别对站点级别熵和可预测性贡献最显著的时不变因素（即在研究期间保持一致的且没有显著变化的特征，如基础设施）。在现有文献的背景下，本研究做出了三个主要贡献：

(1) 我们采用熵和可预测性作为无模型度量，以便更好地研究站点级别固有需求的可预测性。

(2) 通过实证实验，我们进一步确立了这两个度量作为实际预测算法性能的表征，无需进行特征工程和构建预测模型。

(3)通过识别影响单个站点熵和可预测性的关键因素，为系统运营商和城市当局考虑启动新的 BSS 或扩展现有 BSS 提供了管理见解。

本文的后续章节组织如下。第 2 节介绍了所用数据、数据处理方法、需求随机性度量、 基准需求预测算法和评估指标。在第 3 节中， 我们概述了计算出的熵和可预测性。我们还展示了熵/ 可预测性与需求预测模型在单个站点级别上实现的实际表现之间的关联。此外， 我们还确定了影响站点需求的熵和可预测性的最显著因素。最后，第 4 节从结果中得出需求可预测性的推论和启示，讨论了本文局限性，并提出了未来的研究方向。

2.数据与方法

2.1 数据与数据处理

在本研究中，我们的目标是量化各个共享单车站点的自行车借出需求的内在随机性和可预测性，并确定会导致这种随机性的城市因素。为了实现这一目标 ，我们收集了一年的历史Divvy行程记录(共366天，由2015年8月1日至2016年8月1日)作为需求数据。其中每个单次行程的记录包括行程ID 、行程开始和结束时间、借出和归还站点的 ID和名称以及行程持续时间。在我们所的研究时期内，共有534个站点有完整的行程记录。此外，我们将预处理过的历史行程数据划分为两组: 一组用于训练/分析， 跨度为361天， 另一组用于验证，跨度为5天。我们之所以选择芝加哥作为我们的案例研究城市，是因为芝加哥拥有长期的基于站点的BSS运营历史(自2013年开始使用)，而且Divvy的服务覆盖范围很广，覆盖了整个城市的市中心和郊区。每次骑行的开始时间和借出站点的ID都是被提取出来用于本次研究所需的出行记录。随后，我们基于一定的时间间隔(Δt)累计了各个站点各自的借出需求，所用的间隔范围可以从每小时(Δt=1小时)到每天(Δt=24小时)不等， 这是基于之前研究中最常用的聚合情况来确定的(Hulot et al.，2018; Kou and Cai，2021a)。在本研究中，我们选择了4小时的时间间隔(Δt=4小时)作为基准情景，这使得每个站点每天产生6个连续的需求数据点(我们还进行了敏感性分析，以检查使用不同的时间间隔对结果的影响)。因此，我们构建了在1年时间跨度内，站点观察到的一系列借出需求程度，表示为T_i={X_i,1,X_i,2,X_i,3,…,X_i,t,X_i,t+1,…,X_i,T}，其中X_i,t表示在时间点t时累积的借出需求程度。对于534个Divvy站点，我们还获得了它们包括站点 ID、名称、纬度、经度和最大容量在内的数据。我们使用这些站点信息作为源数据来构建表1所列的空间网络变量。此外，我们基于Google Map Places API（应用程序接口），在每个站点周围1000英尺（304.8米）的半径内收集了兴趣点（POIs）。兴趣点包括一系列特定的功能位置，如公交车站、学校和停车场。此外，我们从美国社区调查（US Census Bureau, 2012）的人口普查区划级别获取了社会人口统计数据，特别是人均收入和人口密度。上述准备的空间网络、兴趣点和社会人口统计数据在2.3节中被用来分析对熵和可预测性有贡献的关键因素。

表1. 本研究中使用的站级时不变特征变量的定义

备注:

a) 使用Google Map Places API收集的兴趣点。我们将距离缓冲区设为1000英尺（304.8米），这是人们从共享单车站到兴趣点之间常见的步行范围；

b) 由于BSS随时间安装新站点而不断扩张，车站的空间偏心率会有所变化。因此，我们计算了我们研究时间跨度内的平均空间偏心度；

c) 在本研究中，我们将增量设为0.1英里（161米），并将站点密度的计算限制在0.05英里到4.5英里的范围内，如Kou和Cai (2021b)所建议；

d) 社会人口统计数据是从2017年美国社区调查的人口普查区划级别收集的。如果站点位于该普查区域内，则该普查区域的值被分配给站点。

2.2 需求随机性与可预测性的度量

在BSS需求预测的背景下，预测模型被开发来用于通过线性或非线性方法以统计的方式拟合时空变量与共享单车使用需求之间的关系（Senter, 2008）。预测需求的高低取决于站点需求模式中内在固有的不确定性程度。因此，我们利用信息论中熵（entropy）的概念（Shannon, 1948）来衡量每个站点需求序列中的随机性程度（第2.2.1节）。除了熵，我们还计算了每个站点的可预测性(predictability)，以捕获这些需求可以被正确预测的上限（第2.2.2节）。这两个度量提供了每个安装的共享单车站点需求的内在可预测性的定量评估，这些度量是基于稳定的和相对长期（一年）的需求趋势，而不是各种短期波动（Lu等人，2013）。此外，熵和可预测性显示了站点级理论上未被解释的不确定性的上限以及与给定的需求预测模型相关的潜在误差边界（Song等人，2010）。这两个度量可以基础性地作为站点需求模式的先验无模型评估。

2.2.1 熵

给定每个站点i∈{1,2,3,…,534}观测到的借出需求序列Ti，我们使用由Song 等人(2010) 提出的三种熵的度量来反映使用不同信息获得的站点需求的随机性:

(1)随机熵S_i^rand= log₂N_i，表示站点需求水平的无序性，假设每个需求水平在N_i个唯一的需求水平中以等概率出现(分辨率为每一次自行车借出)。随着随机熵的增加，在某一特定站点中，可能会观察到更多样化的需求水平。

(2) 时间不相关熵

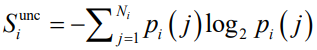
表征了观测到的需求水平的异质性， 其中p_i(j)是在N_i唯一需求水平中观察到第j个需求水平的概率。时间不相关熵既考虑不重复的需求水平的数量， 也考虑它们在某一时间跨度内被观察到的频率。

(3) 实际熵

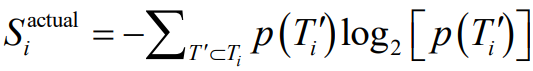
，包含了

一个观测到需求水平的概率以及需求水平被观测到的顺序和观测到的需求水平的持久性(观测到的需求是否在多个时间窗口内保持在特定水平)，其中p(T_i^‘)在观察到的完整序列T_i中找到子序列T_i^‘的概率。由于计算复杂性，实际熵可以基于Lempel-Ziv 数据压缩来估计 (Kontoyiannis 等人，1998)。

2.2.2 可预测性

自然地，具有更大熵的需求序列在其需求模式中具有更多的随机性，这反过来又降低了该站点未来需求的可预测性。考虑到熵(S)表示需求序列的无序性，当具有熵S的一个站点的需求在N个不同水平范围内变动时，预测算法正确预测站点未来需求的可预测性上界(Π)受 Fano 不等式的约束(Fano 和 Hawkins, 1961) (Song et al., 2010):

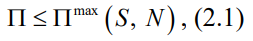
其中Π^max(S,N)与S的关系如式(2.2)所示：

并且式(2.3)描述了二元熵函数:

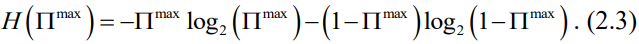
通过基于从一个站点的需求序列中算出的特定N和S来求解式(2.2) 和式(2.3)，我们可以计算可预测性Π。基于第 2.2.1节定义的三种类型的熵，对于每个站点i，我们可以由

此表示随机可预测性

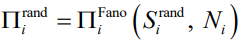
时间不相关可预测性

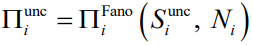
实际可预测性

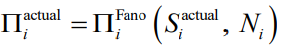
Π的值越高，表明需求可以被更好地预测。通过比较这三种可预测性指标，我们能够查验单个站点的需求序列内的时间相关性如何增强潜在的预测精度 (Lu et al.， 2013)。这也与 Zhou(2015) 和 Lin 等人(2020) 提出的现有工作一致，他们将不同的空间和时间变量纳入预测模型中，旨在减少预测误差。

由于熵和可预测性完全取决于需求本身的时间序列，我们还进行了敏感性分析，以研究每个站点的熵和可预测性如何根据不同的需求观测间隔(Δt)而变化。具体来说，我们计算了六个不同需求观察间隔(Δt)对应的熵和可预测性:1小时、2小时、4小时、6小时、12小时和24小时。这些观察间隔体现了系统操作员对每个站点进行需求监测和分析的潜在粒度。

2.3 站点级别时不变特征

通过历史需求数据可以衡量站点需求的熵和可预测性。然而，对于规划新系统或扩展现有系统以建造新车站，这样的历史需求数据将无法获得。为了检查内在的需求随机性是否与在启动新车站之前就可用的时不变的城市特定特征相关，我们采用了Kou和Cai（2021b）提出的芝加哥个别站点的时不变特征，并分析了这些特征如何影响站点间的熵和可预测性。这些特征列在表1中，它们可以分为三类：土地使用特征、站点的空间网络信息和社会人口统计数据。此外，我们应用了随机森林回归模型来探索时不变变量对每个站点需求的熵和可预测性的重要性。随机森林回归模型是一种机器学习模型，它在数据集的不同子集上训练多个决策树，汇总其结果以提高整体预测性能（Biau和Scornet，2016）。我们选择了这一模型，因为它强大的回归能力以及对因素重要性的可解释性（Belgiu和Dragut，2016）。具体来说，表1中列出的变量用于模型中的输入变量，而在第2.2节中计算的熵（S^rand, S^unc, S^actual）和可预测性（Π^rand, Π^unc, Π^actual）则分别作为因变量。一旦随机森林回归模型被训练，我们就可以根据每个特征在做出正确回归和减少损失方面的贡献提取特征的重要性。这使得理解时间恒定特征对影响需求的熵和可预测性的贡献具有可解释性。这使得理解时不变特征对影响需求的熵和可预测性的贡献具有可解释性。

2.4 基准预测算法和评估指标

第2.2节中讨论的熵和可预测性度量可以确定需求预测算法预测能力的理论上限。为了 验证这些理论上限与站点级别实际预测性能之间的关系，我们使用了两种广泛使用的BSS需求预测基准算法: ARMA和XGBoost。对于与预测算法相关的每个预测性能(参见第 2.4.3 节)，我们对它们的关系进行建模并计算R²分数，这展示了这种关系的适用性。我们还进行了敏感性分析，以检查在使用不同的时间间隔(即分析了第2.2节中描述的六个时间间隔) 时，这种关系是否保持不变， 检查了它们的拟合曲线和相关的R²分数。需要注意的是，我们将预测的输出四舍五入到最接近的整数，因为需求水平(即被借出的单车数量)只能是整数。

2.4.1 ARMA

ARMA算法是一种广泛认可的时间序列预测统计方法，已被应用于各种实际需求预测，如股票价格、库存和疾病感染（Saboia, 1977; Nochai and Nochai, 2006; Chen et al., 2008; Benvenuto et al., 2020）。ARMA模型由两个主要参数组成：p（自回归（AR）的阶数）和q（移动平均（MA）的阶数），表示为ARMA（p, q），相当于没有时间序列差分的ARIMA模型。在时间步长t和在特定车站i时所预测的未来需求X_i,t^pred是过去需求和过去错误的线性组合，公式如下：

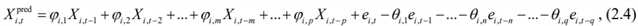
式中，φ_i,m和θ_i,n为系数,e_i,t-n是期望为E[e_i,t-n]=0和方差为σ²的随机噪声,p和q分别为AR和MA多项式的阶数。在我们的研究中，每个站点都有自己的ARMA模型，模型基于站点的历史借出的需求数据(即第2.1节中介绍的训练数据集)上单独训练的，因此，ARMA模型是特定于站点的。此外，每个模型的参数ARMA(p,q)是通过自动ARMA算法确定的(Hyndman and Khandakar, 2008)。

2.4.2 XGBoost

XGBoost是一种树增强机器学习算法，它能够处理具有选定特征的高维数据(Chen and Guestrin, 2016)。在 XGBoost模型中，通过使用树集成模型中的加法函数来预测时间为时的站点的输出预测需求X_i,t^pred:

其中F是回归树的空间; 每个f_k代表K个加法函数中的一个独立树结构；而xi,t对应于时间为t时的车站i的输入变量集。更具体地说，每个车站的输入变量包括表1中描述的时不变变量和天气变量（平均温度、平均湿度、平均风速、平均降水量和平均气压）。

2.4.3 预测算法的评价指标

第2.4.1节和2.4.2节介绍的模型是在训练数据集上进行训练，然后基于测试数据集对其 预测性能进行评估。我们选择了均方根误差(Root Mean Square Error，RMSE)和累积得分（Cumulative Scores，CS)作为性能指标，它们分别代表绝对误差和相对误差。具体而言，RMSE定义为:

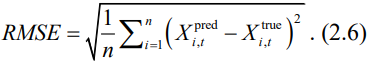
RMSE取值范围为0到+∞。较低的RMSE 分数表明回归模型拟合较好，而较高的RMSE 分数表明预测误差较大。

由于 RMSE受站点容量的影响较大(站点容量越大，RMSE越高)，我们进一步采用Kocer (2013)和Niu et al.(2016) 采用的 CS作为相对预测精度的度量。CS 取值范围为0到1，定义为:

式中D为各站点测试的总时间步数，Dη指的是预测需求值不超过实际需求的上下百分比界限η(%)的数量。在本研究中，我们将百分比界限η设置为10%。CS值越接近 1，表示预测精度越高。

3.结果和讨论

3.1 站点级别需求、熵和可预测性概述

图1(a)显示了在361天的研究期间，每4小时时间间隔内单个车站观察到的需求水平的分布。与之前的研究（例如，Kou和Cai，2019）保持一致，需求分布是长尾的。这表明在每个4小时的窗口内，大多数站点的借出需求较低，而高需求量的站点数量要少得多。

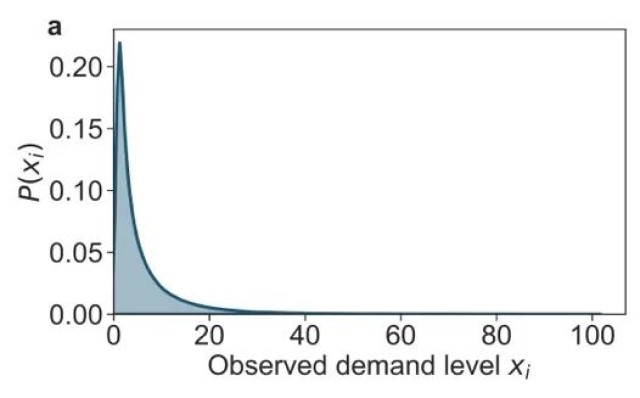
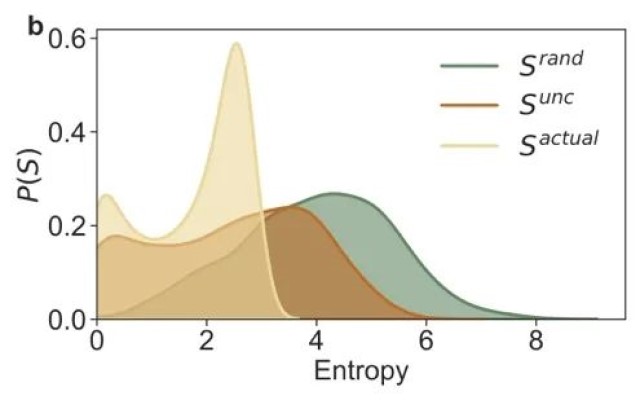
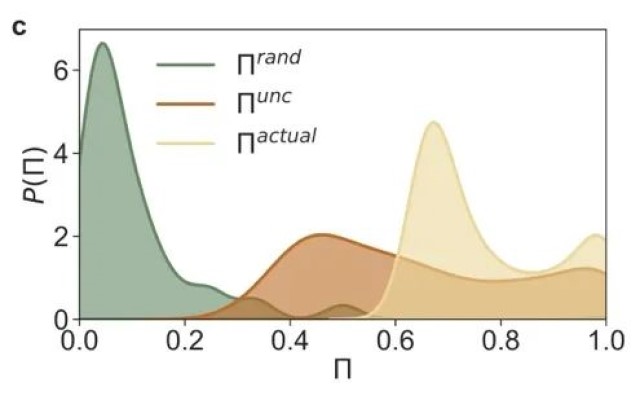
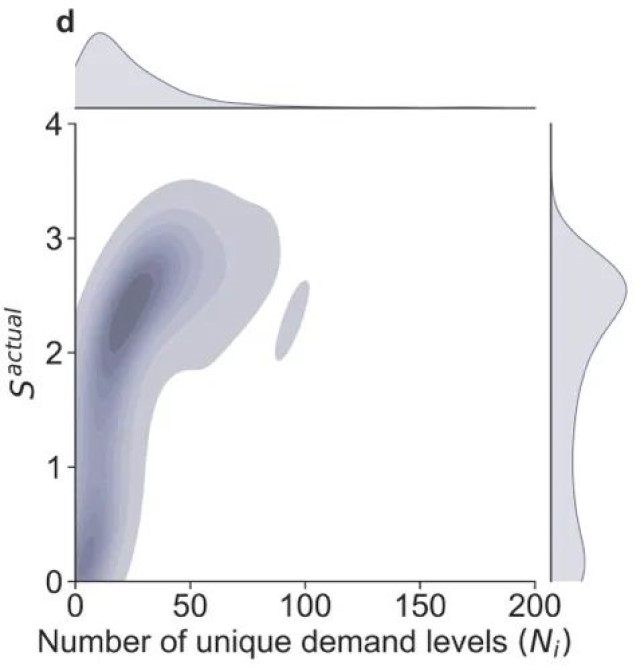
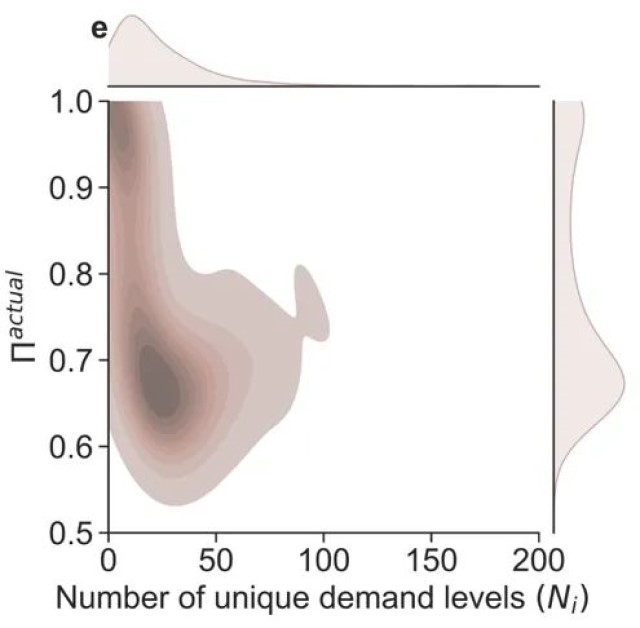
图1. 车站需求及其熵和可预测性概述。(a) 研究期间所有车站观察到的需求水平分布。(b) 随机熵、时间无关熵和实际熵的分布。(c) 随机可预测性、时间无关可预测性和实际可预测性的分布。(d) 车站观察到的独特需求水平数（N_i）和实际熵（S^actual）的联合分布，显示N_i和S^actual之间的相关性。(e) 车站观察到的独特需求水平数（N_i）和实际可预测性（Π^actual）的联合分布，显示N_i和Π^actual之间的相关性。

然而，低需求并不一定意味着低熵或高可预测性。我们根据研究期间各站点的需求序列计算了所有站点的熵和可预测性。图1(b)和1(c)中分别展示了S^rand, S^unc, 和 S^actual以及Π^rand, Π^unc, 和Π^actual的结果分布。S^unc编码了相对于仅考虑唯一需求水平数N_i的S^rand的需求的额外频率信息。这种额外信息解释了需求时间序列中内在的部分随机性，因此p(S^unc)相比p(S^rand)展现出左移（即，一般来说S^unc较低）。同样，S^actual在S^unc的基础上编码了额外的时间顺序信息，所以p(S^actual)比p(S^unc)更向左移。由于p(S^rand)在S^rand≈4处达到峰值，可以预期，如果用户随机在站点借用单车，在一个车站可以平均观察到2S^rand≈16个不同的需求水平。相比之下，实际熵揭示了考虑到可能在车站观察到的需求序列的真实不确定性。令人惊讶的是，实际熵S^actual分别在0.1和2.5处有两个主要峰值。对于S^actual=0.1的车站，它们几乎没有需求不确定性。这些车站的下一个可以预测的需求总是在2^0.1≈1的水平，这表明这些车站可能没有借出需求，但可能随机出现一个借出需求。而对于S^actual=2.5的车站，它们未来的需求可能在2^2.5≈5.66（即小于6）的随机水平。在可预测性方面我们观察到了一致的结论。我们发现，随着更多信息的纳入，个别车站的需求平均而言呈现出Π^actual>Π^unc>Π^rand。大多数车站仅有唯一需求水平数的信息并显示出非常低的可预测性。如图1(c)所示，实际可预测性分布有两个峰值。一组车站对需求几乎具有完美的可预测性，这与我们的观察相符，即这些车站几乎没有借出需求。另一组车站的可预测性在0.65左右。换句话说，无论预测算法表现多么优秀，Π^actual=0.65的车站的未来需求水平的最大预测准确率为65%。因此，Π^actual可作为个别车站可预测性的内在限制。值得注意的是，S^actual和Π^actual的双峰分布表明了车站中的需求可预测性两极分化。尽管总体的车站的需求在各站点间非常低，但有相当数量的车站表现出高熵和降低的可预测性。这意味着系统运营商应特别关注这些车站。

我们绘制了图1(d)和1(e)，以进一步调和这一矛盾：总体上，车站的观测需求较低，但S^actual和Π^actual的分布中有两个峰值。对于可预测性低（熵高）的车站群，它们有跨越了从0到大约100的广泛的历史观测需求唯一水平。特别是，其中唯一需求水平的峰值平均对应于30。相反，高可预测性（低熵）相关的车站覆盖了从0到大约25的较窄独特水平范围，平均为1。因此，虽然这两组车站都可能经历低水平的需求，但高熵群体内的车站可以预期呈现更广泛的需求变化。个别车站需求范围变化的增加引入了更多的随机性到观测需求的时间序列中，从本质上导致了更高的熵和更低的可预测性。此外，极化车站的对比也在图2中展示，该图显示了具有不同S^actual和Π^actual的车站的整体空间分布。高S^actual但低Π^actual的车站（深红色的小圆圈）主要位于市中心区域，而低S^actual但高Π^actual的车站（深蓝色的大圆圈）主要分布在郊区。

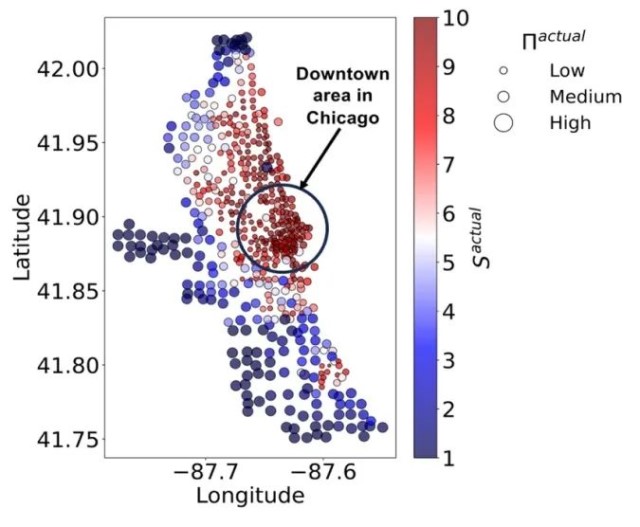
图 2. 芝加哥不同实际熵S^actual和实际可预测性的站点分 布(每个圆圈代表一个站点)。

3.2 熵/可预测性与预测性能的关系

在本节中，我们确认熵和可预测性(衡量根植于车站需求的随机性) 分别是实证预测误差和需求预测模型精度的可行的且无模型的估计量。

在图3(a)至3(f)中，每个数据点的RMSE代表来自每个预测算法的每个车站测试时的平均RMSE。结果显示了个别车站一年历史需求的熵与未来需求预测所得RMSE值之间存在指数关联。这种关系在将S^rand和RMSE相关联时，对于使用ARMA算法的R²=0.94，对于使用XGBoost算法的R²=0.88。同样，图3(g)至3(l)展示了需求可预测性与CS值之间建立的逻辑关系，其中使用ARMA算法得到的CS与Π之间R²变化范围为0.81至0.87，而使用XGBoost算法得到的的CS与Π之间R²变化范围为0.59至0.74。需要注意的是，我们将RMSE与熵配对，将CS与可预测性配对，因为每对值使用了相同的度量单位。RMSE和熵以错误的绝对大小表示，而CS和可预测性以准确性的百分比表示。

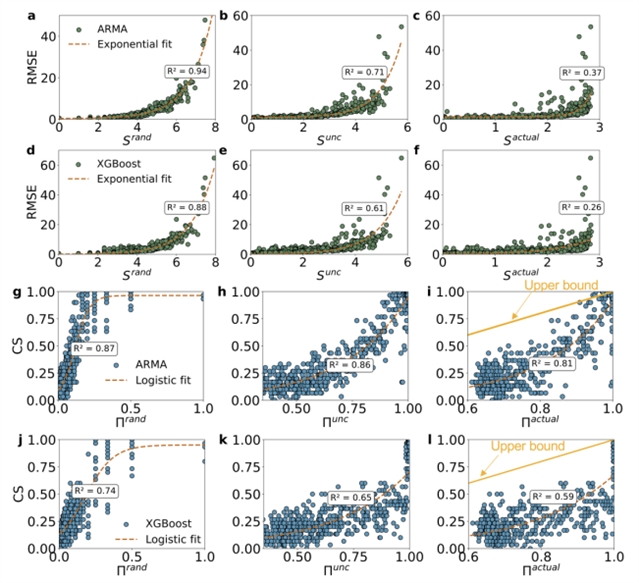
图3. (a) - (f)为熵与 RMSE 的相关关系；(g) - (l)表示可预测性与 CS 之间的相关性；(i)和(l)中的橙色边界线表明，每个站点的预测模型的实际 CS低于其理论可预测性。

图3(i)和3(l)验证了可预测性作为预测准确性的理论极限，这与Lu等人（2013）确定的上限一致。熵和可预测性捕捉了BSS需求预测所获的的预测分析的理论极限，为此类BSS需求数据提供了一个可接近的预测能力上限。例如，对于平均Π^actual=0.65的车站群，在ARMA和XGBoost模型中，它们的CS值都保持在0.5以下。尽管有些车站预期可以达到最大Π^actual=0.8，但它们仍然表现出实际CS值低于0.5，验证了Π^actual表明了实证预测准确性的界限。这与图3(i)和3(l)中显示的数据点分布一致，即预测模型中对应的实际CS总是小于理论可预测性。也就是说，通过在所有车站应用相同的需求预测模型，并对某些变量进行回归以预测站点级别的需求，可以预期不同车站的各种预测误差受到其固有可预测性的限制。此外，值得注意的是，熵和可预测性是无模型估计器，因为它们完全源于各个车站的历史需求。它们的计算独立于任何预测模型，并作为先验测量，代替预测模型输入变量的广泛特定领域特征工程。

3.3 特征对熵和可预测性的影响

在验证熵和可预测性是可行的、无模型的实际预测效果的表征后，我们进一步确定了哪些时不变因素对车站需求的熵和可预测性贡献最大。在这项工作中，我们运行了随机森林回归模型，其输入是表1中列出的时不变变量，其输出是熵的集合（S^rand, S^unc, S^actual）或可预测性的集合（Π^rand,Π^unc, Π^actual）。基于五折交叉验证，我们的结果显示该模型对熵的RMSE为0.66，对可预测性的RMSE为0.83。这突出显示了时不变因素与车站需求的熵/可预测性之间存在统计显著关系。

在表2中，我们分别列出了影响熵和可预测性的三个最重要的时间恒定属性（详见补充信息A1和A2中的特征重要性排名完整列表）。我们的发现表明，人均收入、空间偏心率和停车场数量对熵和可预测性都很重要。值得注意的是，这三个最显著的变量中的每一个都来自不同的变量类别：人均收入是社会人口统计变量；空间偏心度是空间网络变量；停车场数量是土地使用变量。

表2. 显著的时不变变量及其在熵/可预测性模型中的特征重要性

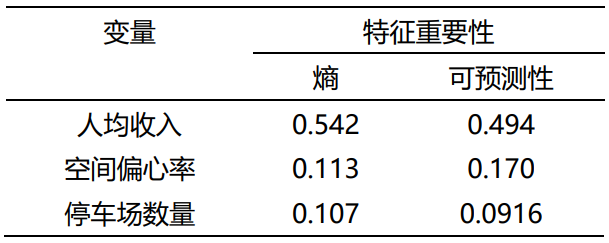
在图4中，我们展示了实际可预测性Π^actual最高和最低的前十个车站的这三个确定了的时不变变量的具体数值，以检验变量对熵和可预测性的正面/负面影响。可以观察到，人均收入对可预测性产生负面影响，因为可预测性较低的车站表现出更高的人均收入。同样，停车场数量也对可预测性产生负面影响。另一方面，空间偏心率对可预测性产生正面影响，偏心度更高的车站表现出更高的可预测性。此外，在图5中，我们描述了整个系统中车站的空间分布及其相关的三个时不变变量，展示了服务区域内熵和可预测性与这三个变量之间的空间相互作用。对于人均收入（图5(a)），我们观察到，如图2所示，表现出更高可预测性和更低熵的车站通常位于人均收入较低的郊区。相反，可预测性较低的车站通常位于人均收入较高的市中心区域。在空间偏心率方面，可以观察到，在郊区，需求可预测性较高的车站与邻近车站相距较远。相反，需求可预测性较低的车站往往集中在城市中心，那里的车站更密集。另外，对于停车场，与可预测性较高、熵较低的车站相比，可预测性较低的车站位于在市中心拥有更多的停车场的区域周围。

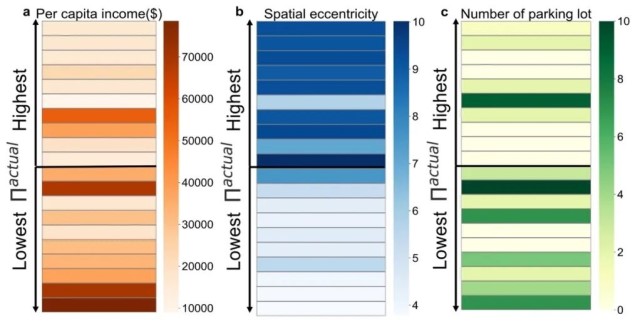
图4. 实际可预测性（Π^actual）最高和最低前 10 位车站的属性(a)人均收入、 (b)空间偏心率、( c) 停车场数量

图5. 按(a)人均收入、(b)空间偏心率、(c)停车场数量划分的车站空间分布。

影响熵和可预测性的重要城市或系统特定的时不变变量可以通过几种方式解释。从人均收入的重要性来看，我们可以推断，在较高财富的人口普查区域，更多的车站可能服务于基于休闲的或娱乐的出行（Stromberg, 2015），这将导致比服务于常规通勤或差事的车站更高的熵。另一方面，高收入区域的高熵可能预示着高人均收入下各种交通方式可达性（Smith等人，2020），这些地方有更多种类的出行和选择。空间偏心度表明了那些离其他车站更远的车站更可预测。也就是说，郊区车站的需求通常更可预测。这可能是由于郊区地方对多种出行目的的可达性较低，或者可能代表郊区车站的整体使用率较低。停车位的数量可能表明一个地区接纳各种出行目的的能力。图5(c)显示停车场主要集中在市中心区域。考虑到BSS在第一/最后一公里出行中的功能，顾客可以将他们的私家车停在停车位（例如，公共停车场和街道停车），并继续在市中心地区使用共享单车进行后续出行。这种接纳各种出行的能力增加了在市中心地区可以预期的出行数量的变化，从而导致高熵，并进而降低需求的可预测性。

3.4 敏感性分析

3.4.1 不同观测间隔下的熵和可预测性

在不同的需求观测间隔下，熵和可预测性分布不同。图6显示了需求观测频率的明显影响: 增加需求观测的频率可以提高那些最初可预测性低的车站的可预测性，并降低它们的熵。然而，这种观测频率的增加似乎对那些已经显示出高预测性的车站没有影响。更具体地，在图6(a)和6(d)中，随着观测频率的降低，站点的S^rand值倾向于更高，而Π^rand值倾向于更低。这是因为在较低频率的监测的情况下，需求会累积到更高的水平。例如，连续两小时内的每小时一个单位的需求水平可能累积到两小时观测窗口内的所记录的两个单位的需求水平。这也与图6(g)中显示的P(X_i)的分布一致，当进行更频繁的监测时，峰值略微向零移动，并且分布的方差减小。此外，在图6(b)、6(c)、6(e)和6(f)中，可以观察到，高可预测性车站（即低熵车站）的峰值在监测频率变化时保持一致。这是因为这些站点通常与非常低的需求水平（通常为0或1）相关，即使监测从每小时变化到每天，需求的时间序列也保持不变。相反，值得注意的是，当将监测间隔从24小时降低到1小时时，低可预测性车站的峰值会向更高的可预测性转移。

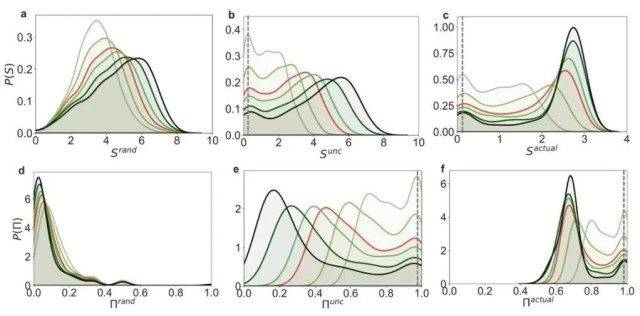
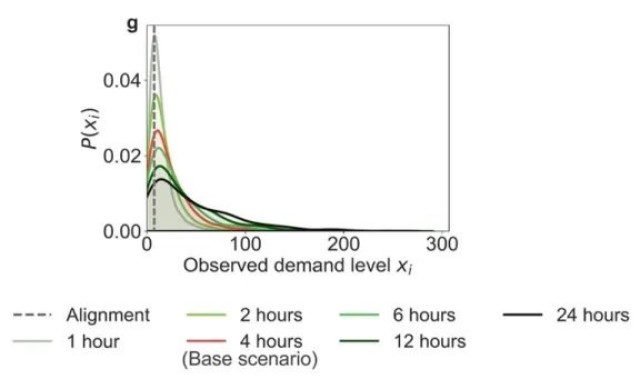
图6. (a)至(c)为熵，(d)至(f)为可预测性，以及(g)为在不同需求观测间隔下的需求水平分布。

这种敏感性分析还提供了潜在的操作策略，以减轻与某些站点相关的低可预测性。运营商可以在不同地点的站点异质性地监测需求：市中心区域可能需要更频繁的监测（例如每半小时或每小时一次）；相反，郊区可能只需较少频繁的观测（例如每12小时或每天一次）。通过缩短需求观测之间的时间间隔，需求的时间序列趋于不那么随机，因此运营商可以在其预测模型中预期到更准确的预测结果和较少的错误。这种策略还提出了一种实用的方法，用于平衡不同服务区域的运营资源，同时保持服务的可靠性和可预测性。

3.4.2 不同观测间隔下理论上限与实际预测性能的关系

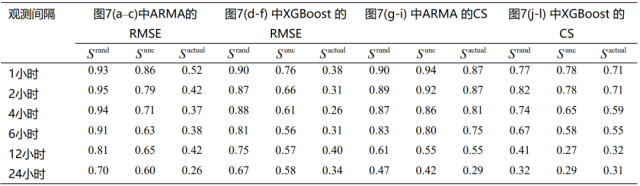
我们的敏感性分析巩固了第3.2节中确定的熵/可预测性（即理论上限）与RMSE/CS（即实际预测性能）之间的关系。图7展示了不同观测间隔下两种预测算法及其性能指标的拟合曲线，表3列出了图7中每个拟合曲线的相关R²分数。与图3相同，RMSE和熵呈指数关系，而CS和可预测性之间的关系是逻辑关系。当更频繁地监测需求时（时间间隔较小），相应拟合曲线的R²分数变得更高。这是因为在给定的固定时期内（例如，在本研究中为366天），更高频率的观测产生了更多的数据点用于训练和测试模型，使模型得到了更好的训练。

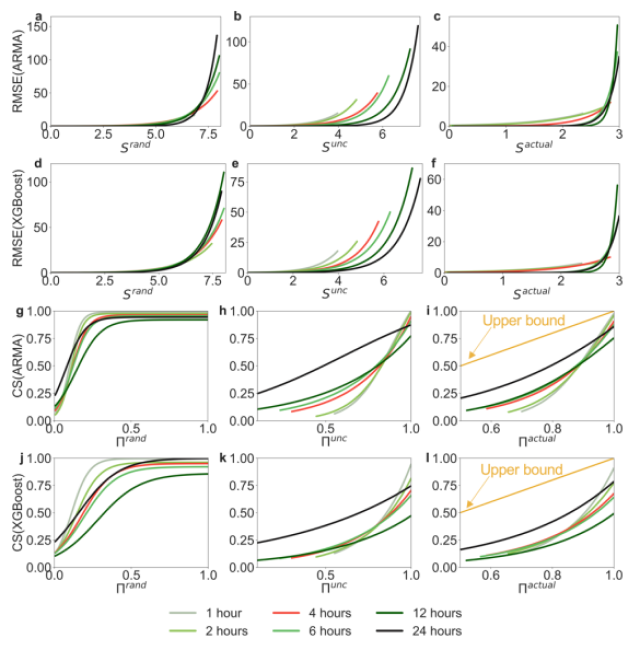
图7. 不同需求观测间隔下的关系 (a) - (c) ARMA和三种熵的RMSE、(d) -(f) XGBoost和三种熵的RMSE、(g) -(i) ARMA和三种可预测性的CS、(j) -(l) XGBoost和三种可预测性的的CS。

表3. 图7中拟合曲线的分数

4.结论

总结来说，本研究通过基于信息论的熵和可预测性测量了站点需求的固有随机性。我们将这些指标与经验性表现指标进行了验证，以表明熵和可预测性适用于作为无模型估计器，以期望预测模型中的误差和准确性。此外，我们确定了三个最重要的时不变因素——人均收入、空间偏心率和停车场数量——这些因素影响站点需求的熵和可预测性。我们从这项研究中得到的结果可以作为BSS管理、运营、扩展和启动的先验建议，而无需特定领域的特征工程和建模需求预测算法。

对于拥有活跃BSS的城市，我们的发现意味着存在着现有的预测模型可能无法捕捉内在的错误和随机性，因此运营商可以在不同的服务区域应用定制的监控策略，以提高需求的可预测性和服务的可靠性。例如，对于熵高而可预测性低的车站，可以更频繁地使用监控和维护（例如再平衡），以提高运营功能。另一方面，对于考虑扩展或投资BSS的城市，与高熵站点相关的所确定的时不变关键因素可以在决定向BSS添加新站点时被定性考虑。此外，在站点级别测量熵和可预测性允许在站点之间进行更精细的运营，并提供了提高每个车站量身定制的管理的可能性。因此，这些结果对运营商在站点监控、再平衡、容量设计、选址或退出方面的决策有直接影响。

更广泛而言，对于没有BSS的城市，市政管理者和潜在的系统运营商可以通过熵和可预测性这一媒介将时不变的城市和系统特性与潜在的需求预测效能联系起来。这些先验测量可以帮助指导未来BSS及其相关基础设施（如停车场和自行车道）的规划和设计。我们的模型也是自适应的，因此当时不变的城市特性发生重大变化时，运营商可以重新进行模型计算，以更新他们下一阶段的规划决策。

对这项研究下一阶段的建议是：1) 进行大规模分析，以将熵和可预测性推广到其他城市中；2) 在更多的预测算法上将熵和可预测性与其他评估指标进行比较（这些指标可能更强调预测误差发生的频率而不是多少）。在第一种情况下，BSS需求预测性能可能会受到特定系统中高熵站点数量的重大影响，因此案例研究选择和结果推广必须考虑BSS的这一方面。大规模分析可以帮助确定这些方法的推广可能性，并提供更多关于全世界各个BSS动态的见解。在第二种情况下，了解需求预测的错误频率与错误程度同样重要，特别是对于自行车的动态再平衡。因此，一种捕捉需求的时间预测误差的评估指标可能在关联本研究所计算的不同形式的熵和可预测性方面有用。此外，我们在第3.2节结果中发现的指数和逻辑关联与熵有关的文献中识别的线性关联略有不同。调查这一现象的原因是未来研究的一个方向。

BSS需求预测研究中的一个挑战是缺乏出行目的数据。在不知道共享单车站点的出行目的的情况下，预测需求会变得更加困难。站点的高熵可能表明出行目的的多样性和异质性，而低熵的站点可能意味着为了类似的旅行目的而使用 BSS的一致旅行者。当出行目的数据可获取时，未来的研究可以探索熵与出行目的之间的关系以及如何用于预测需求。此外，未来的研究可以更详细地探索高熵站与低熵站的运营成本。如果熵测量与车站维护成本之间存在关系，我们的方法可以用来预测增加新站点的运营成本，或者在尚未拥有已投入使用的BSS的城市中投资BSS。

参考文献

Bachand-Marleau J, Lee B, El-Geneidy A (2012). Better understanding of factors influencing likelihood of using shared bicycle systems and frequency of use. Transportation Research Record: Journal of the Transportation Research Board, 2314(1): 66–71 doi:10.3141/2314-09

Bao J, Xu C, Liu P, Wang W (2017). Exploring bikesharing travel patterns and trip purposes using smart card data and online point of interests. Networks and Spatial Economics, 17(4): 1231–1253 doi:10.1007/s11067-017-9366-x

Belgiu M, Dr?gu? L (2016). Random forest in remote sensing: A review of applications and future directions. ISPRS Journal of Photogrammetry and Remote Sensing, 114: 24–31 doi:10.1016/j.isprsjprs.2016.01.011

Benvenuto D, Giovanetti M, Vassallo L, Angeletti S, Ciccozzi M (2020). Application of the ARIMA model on the COVID-2019 epidemic dataset. Data in Brief, 29: 105340 doi:10.1016/j.dib.2020.105340

Biau G, Scornet E (2016). A random forest guided tour. Test, 25(2): 197–227 doi:10.1007/s11749-016-0481-7

Cazabet R, Borgnat P, Jensen P (2017). Using degree constrained gravity null-models to understand the structure of journeys’ networks in bicycle sharing systems. In: 25th European Symposium on Artificial Neural Networks, Computational Intelligence, and Machine Learning. Bruges: ENSANN, 25

Chai D, Wang L, Yang Q (2018). Bike flow prediction with multi-graph convolutional networks. In: Proceedings of the 26th ACM SIGSPATIAL InternationalConference on Advances in Geographic Information Systems. Seattle, WA: ACM, 397–400

Chen L, Zhang D, Wang L, Yang D, Ma X, Li S, Wu Z, Pan G, Nguyen T, Jakubowicz J (2016). Dynamic cluster-based over-demand prediction in bike sharing systems. In: Proceedings of the InternationalJoint Conference on Pervasive and Ubiquitous Computing. Heidelberg: ACM, 841–852

Chen P, Yuan H, Shu X (2008). Forecasting crime using the ARIMA model. In: 5th InternationalConference on Fuzzy Systems and Knowledge Discovery. Jinan: IEEE, 627–630

Chen T, Guestrin C (2016). Xgboost: A scalable tree boosting system. In: Proceedings of the 22nd ACM SIGKDD InternationalConference on Knowledge Discovery and Data Mining. San Francisco, CA: ACM, 785–794

El-Assi W, Salah Mahmoud M, Nurul Habib K (2017). Effects of built environment and weather on bike sharing demand: A station level analysis of commercial bike sharing in Toronto. Transportation, 44(3): 589–613 doi:10.1007/s11116-015-9669-z

El Sibai R, Chabchoub Y, Fricker C (2018). Using spatial outliers detection to assess balancing mechanisms in bike sharing systems. In: 32nd InternationalConference on Advanced Information Networking and Applications (AINA). Krakow: IEEE, 988–995

Fano R, Hawkins D (1961). Transmission of information: A statistical theory of communication. American Journal of Physics, 29(11): 793–794 doi:10.1119/1.1937609

Fishman E (2016). Bikeshare: A review of recent literature. Transport Reviews, 36(1): 92–113 doi:10.1080/01441647.2015.1033036

Fishman E, Allan V (2019). Chapter six: Bike share. In: Fishman E, ed. Advances in Transport Policy and Planning. Volume 4. The Sharing Economy and the Relevance for Transport. Cambridge: Elsevier Inc., 121–152

He S, Shin K (2020). Towards fine-grained flow forecasting: A graph attention approach for bike sharing systems. In: Proceedings of the Web Conference.Taipei: ACM, 88–98

Hulot P, Aloise D, Jena S (2018). Towards station-level demand prediction for effective rebalancing in bike-sharing systems. In: Proceedings of the ACM SIGKDD InternationalConference on Knowledge Discovery and Data Mining. London: ACM, 378–386

Hyland M, Hong Z, Pinto H, Chen Y (2018). Hybrid cluster-regression approach to model bikeshare station usage. Transportation Research Part A: Policy and Practice, 115: 71–89 doi:10.1016/j.tra.2017.11.009

Hyndman R, Khandakar Y (2008). Automatic time series forecasting: The forecast package for R. Journal of Statistical Software, 27(3): 1–22 doi:10.18637/jss.v027.i03

Jia W, Tan Y, Liu L, Li J, Zhang H, Zhao K (2019). Hierarchical prediction based on two-level Gaussian mixture model clustering for bike-sharing system. Knowledge-Based Systems, 178: 84–97 doi:10.1016/j.knosys.2019.04.020

Kim D, Cho Y, Kim D, Park C, Choo J (2022). Residual correction in real-time traffic forecasting. In: Proceedings of the 31st ACM InternationalConference on Information & Knowledge Management. Atlanta, GA: ACM, 962–971

Kocer U U (2013). Forecasting intermittent demand by Markov chain model. InternationalJournal of Innovative Computing, Information & Control, 9(8): 3307–3318

Kontoyiannis I, Algoet P, Suhov Y, Wyner A (1998). Nonparametric entropy estimation for stationary processes and random fields, with applications to English text. IEEE Transactions on Information Theory, 44(3): 1319–1327 doi:10.1109/18.669425

Kou Z, Cai H (2019). Understanding bike sharing travel patterns: An analysis of trip data from eight cities. Physica A, 515: 785–797 doi:10.1016/j.physa.2018.09.123

Kou Z, Cai H (2021a). Comparing the performance of different types of bike share systems. Transportation Research Part D: Transport and Environment, 94: 102823 doi:10.1016/j.trd.2021.102823

Kou Z, Cai H (2021b). Incorporating spatial network information to improve demand prediction for bike share system expansion. In: Proceedings of the 10th InternationalWorkshop on Urban Computing. Beijing

Kou Z, Wang X, Chiu S, Cai H (2020). Quantifying greenhouse gas emissions reduction from bike share systems: A model considering real-world trips and transportation mode choice patterns. Resources, Conservation and Recycling, 153: 104534 doi:10.1016/j.resconrec.2019.104534

Li Y, Zheng Y (2020). Citywide bike usage prediction in a bike-sharing system. IEEE Transactions on Knowledge and Data Engineering, 32(6): 1079–1091 doi:10.1109/TKDE.2019.2898831

Li Y, Zheng Y, Zhang H, Chen L (2015). Traffic prediction in a bike-sharing system. In: Proceedings of the 23rd SIGSPATIAL InternationalConference on Advances in Geographic Information Systems. Seattle, WA: ACM, 1–10

Lin L, He Z, Peeta S (2018). Predicting station-level hourly demand in a large-scale bike-sharing network: A graph convolutional neural network approach. Transportation Research Part C: Emerging Technologies, 97: 258–276 doi:10.1016/j.trc.2018.10.011

Lin P, Weng J, Hu S, Alivanistos D, Li X, Yin B (2020). Revealing spatio-temporal patterns and influencing factors of dockless bike sharing demand. IEEE Access, 8: 66139–66149 doi:10.1109/ACCESS.2020.2985329

Liu C, Gao X, Wang X (2022). Data adaptive functional outlier detection: Analysis of the Paris bike sharing system data. Information Sciences, 602: 13–42 doi:10.1016/j.ins.2022.04.029

Lu X, Wetter E, Bharti N, Tatem A, Bengtsson L (2013). Approaching the limit of predictability in human mobility. Scientific Reports, 3(1): 2923 doi:10.1038/srep02923

Luo H, Zhao F, Chen W, Cai H (2020). Optimizing bike sharing systems from the life cycle greenhouse gas emissions perspective. Transportation Research Part C: Emerging Technologies, 117: 102705 doi:10.1016/j.trc.2020.102705

Médard de Chardon C, Caruso G (2015). Estimating bike-share trips using station level data. Transportation Research Part B: Methodological, 78: 260–279 doi:10.1016/j.trb.2015.05.003

Niu Z, Zhou M, Wang L, Gao X, Hua G (2016). Ordinal regression with multiple output CNN for age estimation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV: IEEE, 4920–4928

Nochai R, Nochai T (2006). ARIMA model for forecasting oil palm price. In: Proceedings of the 2nd IMT-GT Regional Conference on Mathematics, Statistics and Applications. Penang: Academia, 13–15

Regue R, Recker W (2014). Proactive vehicle routing with inferred demand to solve the bikesharing rebalancing problem. Transportation Research Part E: Logistics and Transportation Review, 72: 192–209 doi:10.1016/j.tre.2014.10.005

Saboia J L M (1977). Autoregressive integrated moving average (ARIMA) models for birth forecasting. Journal of the American Statistical Association, 72(358): 264–270 doi:10.1080/01621459.1977.10480989

Senter H (2008). In: Kutner M H, Nachtsheim C J, Neter J, Li W, eds. Applied Linear Statistical Models. 5th ed. Boston: McGraw-Hill

Shaheen S, Guzman S, Zhang H (2010). Bikesharing in Europe, the Americas, and Asia. Transportation Research Record: Journal of the Transportation Research Board, 2143(1): 159–167 doi:10.3141/2143-20

Shannon C E (1948). A mathematical theory of communication. Bell System Technical Journal, 27(3): 379–423 doi:10.1002/j.1538-7305.1948.tb01338.x

Singhvi D, Singhvi S, Frazier P I, Henderson S G, Mahony E O, Shmoys D B, Woodard D B (2015). Predicting bike usage for New York City’s bike sharing system. In: AAAI Workshop: Computational Sustainability. Austin, TX: AAAI

Smith D A, Shen Y, Barros J, Zhong C, Batty M, Giannotti M (2020). A compact city for the wealthy? Employment accessibility inequalities between occupational classes in the London metropolitan region 2011. Journal of Transport Geography, 86: 102767 doi:10.1016/j.jtrangeo.2020.102767

Song C, Qu Z, Blumm N, Barabási A L (2010). Limits of predictability in human mobility. Science, 327(5968): 1018–1021 doi:10.1126/science.1177170

Straits Research (2021). Bike sharing market new research analysis and forecast 2030. Online Report

Stromberg J (2015). Bike share users are mostly rich and white. Here’s why that’s hard to change

US Census Bureau (2012). 2009–2011 American Community Survey 3-year Public Use Microdata Samples

Yang Z, Chen J, Hu J, Shu Y, Cheng P (2019). Mobility modeling and data-driven closed-loop prediction in bike-sharing systems. IEEE Transactions on Intelligent Transportation Systems, 20(12): 4488–4499 doi:10.1109/TITS.2018.2886456

Yang Z, Hu J, Shu Y, Cheng P, Chen J, Moscibroda T (2016). Mobility modeling and prediction in bike-sharing systems. In: Proceedings of the 14th Annual InternationalConference on Mobile Systems, Applications, and Services. Singapore: ACM, 165–178

Yu B, Yin H, Zhu Z (2018). Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. In: Proceedings of the 27th InternationalJoint Conference on Artificial Intelligence. Stockholm: ACM, 3634–3640

Zhang Y, Thomas T, Brussel M J G, van Maarseveen M F A M (2016). Expanding bicycle-sharing systems: Lessons learnt from an analysis of usage. PLoS One, 11(12): e0168604 doi:10.1371/journal.pone.0168604

Zheng V Z, Choi S, Sun L (2023). Enhancing deep traffic forecasting models with dynamic regression. arXiv preprint, arXiv:2301.06650

Zhou X (2015). Understanding spatiotemporal patterns of biking behavior by analyzing massive bike sharing data in Chicago. PLoS One, 10(10): e0137922 doi:10.1371/journal.pone.0137922

Zhou Y, Wang L, Zhong R, Tan Y (2018). A Markov chain based demand prediction model for stations in bike sharing systems. Mathematical Problems in Engineering, 8028714 doi:10.1155/2018/8028714

Zhou Y, Yu Y, Wang Y, He B, Yang L (2023). Mode substitution and carbon emission impacts of electric bike sharing systems. Sustainable Cities and Society, 89: 104312 doi:10.1016/j.scs.2022.104312

推荐阅读

1.FEM Dec 2023, Volume 10 Issue 4 内容摘要

2.FEM Sep 2023, Volume 10 Issue 3 内容摘要

3.FEM Jun 2023, Volume 10 Issue 2内容摘要

4.FEM 2023, Volume 10 Issue 1 后疫情时代供应链韧性的提升专题内容摘要

5.高铁企业国际声誉的形成机理

6.助推家庭用能转向可持续消费模式：来自行为经济学的见解

7.FTS解需求可拆分的车辆路径问题（SDVRPs）

8.未来城市交通管理

9.从价值增值视角探索工程建造服务化的转型途径

10.PPP是否仍然是解决社会基础设施问题的好方法？系统的文献综述

《前沿》系列英文学术期刊

由教育部主管、高等教育出版社主办的《前沿》（Frontiers）系列英文学术期刊，于2006年正式创刊，以网络版和印刷版向全球发行。系列期刊包括基础科学、 、工程技术和人文社会科学四个主题，是我国覆盖学科最广泛的英文学术期刊群，其中13种被SCI收录，其他也被A&HCI、Ei、MEDLINE或相应学科国际权威检索系统收录，具有一定的国际学术影响力。系列期刊采用在线优先出版方式，保证文章以最快速度发表。

中国学术前沿期刊网

http://journal.hep.com.cn