论文标题：Follow the perturbed approximate leader for solving semi-bandit combinatorial optimization (求解半老虎机组合优化的 Follow Perturbed Approximate Leader 算法)

期刊：Frontiers of Computer Science

作者：Feidiao YANG, Wei CHEN , Jialin ZHANG , Xiaoming SUN

发表时间：30 Aug 2021

DOI：10.1007/s11704-020-9519-9

微信链接：点击此处阅读微信文章

导读

面对不确定性的组合优化在运筹学和机器学习中都是重要的挑战。在本文中，我们考虑该研究方向上一类特殊而重要的问题。它们被称为半老虎机反馈对抗在线组合优化问题，简称对抗组合半老虎机问题。在该类问题中，算法重复地做出组合决策并且获得相应的反馈。已有的算法往往关注悔界的保证或者假设问题存在一个高效的离线黑盒。但当相应的离线组合优化问题是NP-难的时候，如何高效地求解相应的在线组合优化问题仍然是一大挑战。在本文中，我们提出了Follow-the-Perturbed-Leader (FPL)算法的一个变种以解决这个问题。与已有的FPL算法不同，我们的方法采用了近似算法作为离线黑盒并且通过加上非负随机噪声的方式来扰动数据。我们的方法是简单高效的。此外，对一类有FPTAS (全多项式时间近似方案)的重要组合优化问题，我们的方法能保证次线性的松弛悔界。除上述理论分析以外，我们还进行了一系列的实验来验证我们算法的性能。

文章精要

摘要

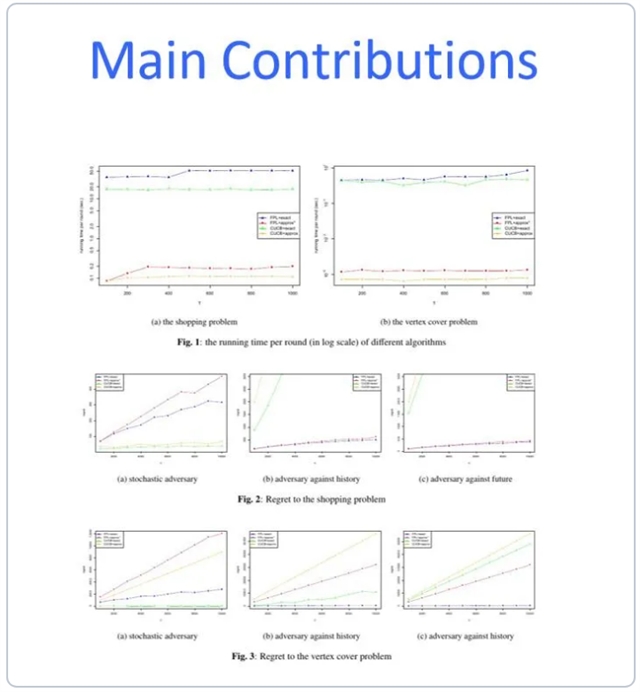
Combinatorial optimization in the face of uncertainty is a challenge in both operational research and machine learning. In this paper, we consider a special and important class called the adversarial online combinatorial optimization with semi-bandit feedback, in which a player makes combinatorial decisions and gets the corresponding feedback repeatedly. While existing algorithms focus on the regret guarantee or assume there exists an efficient offline oracle, it is still a challenge to solve this problem efficiently if the offline counterpart is NP-hard. In this paper, we propose a variant of the Followthe-Perturbed-Leader (FPL) algorithm to solve this problem. Unlike the existing FPL approach, our method employs an approximation algorithm as an offline oracle and perturbs the collected data by adding nonnegative random variables. Our approach is simple and computationally efficient. Moreover, it can guarantee a sublinear (1+ ε)-scaled regret of order O(T23T23) for any small ε>0 for an important class of combinatorial optimization problems that admit an FPTAS (fully polynomial time approximation scheme), in which Tis the number of rounds of the learning process. In addition to the theoretical analysis, we also conduct a series of experiments to demonstrate the performance of our algorithm.

相关内容推荐：

L3-值命题逻辑的单调Gentzen推理系统和非单调Gentzen推理系统 2021 15(3)：153401

【FCS 理论计算科学专栏】严格d-正则随机(3,2s)-SAT问题的可满足阈值性质 2020 14(6)：146406

【FCS 理论计算科学专栏】以CCSL为规约语言的时空一致性语言的验证框架 2020 14(1)：105-129

Frontiers of Computer Science （FCS）是由教育部主管、高等教育出版社和北京航空航天大学共同主办、SpringerNature 公司海外发行的英文学术期刊。本刊于 2007 年创刊，双月刊，全球发行。主要刊登计算机科学领域具有创新性的综述论文、研究论文等。本刊主编为周志华教授，共同主编为熊璋教授。编委会及青年 AE 团队由国内外知名学者及优秀青年学者组成。本刊被 SCI、Ei、DBLP、INSPEC、SCOPUS 和中国科学引文数据库（CSCD）核心库等收录，为 CCF 推荐期刊；两次入选“中国科技期刊国际影响力提升计划”；入选“第4届中国国际化精品科技期刊”；入选“中国科技期刊卓越行动计划项目”。

《前沿》系列英文学术期刊

由教育部主管、高等教育出版社主办的《前沿》（Frontiers）系列英文学术期刊，于2006年正式创刊，以网络版和印刷版向全球发行。系列期刊包括基础科学、 、工程技术和人文社会科学四个主题，是我国覆盖学科最广泛的英文学术期刊群，其中13种被SCI收录，其他也被A&HCI、Ei、MEDLINE或相应学科国际权威检索系统收录，具有一定的国际学术影响力。系列期刊采用在线优先出版方式，保证文章以最快速度发表。

高等教育出版社入选“中国科技期刊卓越行动计划”集群化项目。Frontier系列期刊中：13种被SCI收录；1种被A&HCI收录；6种被Ei收录；2种被MEDLINE收录；11种中国科技核心期刊；16种被CSCD收录。

中国学术前沿期刊网

http://journal.hep.com.cn